|
|
1.IntroductionVanishing point (VP) is defined as the convergence point of projected parallel lines in an image plane.1 When a set of parallel lines in three-dimensional (3-D) space is projected onto a set of parallel or nonparallel lines in the two-dimensional (2-D) plane, the VP lies at infinity or at some finite distance, respectively. The VP is an invariant feature that provides important cues for inferring the 3-D structure of a real scene. Therefore, it is widely relevant to robotic navigation, visual measurement, camera calibration,2 3-D reconstruction, augmented reality, image understanding, and similar fields. Naturally, VP detection has been an important topic in the computer vision research community. In this work, we propose a bioinspired scheme for detecting VPs. Our solution directly detects all possible nonorthogonal VPs in the image plane, without reliance on camera calibration parameters. Our algorithm offers several advantages over previous algorithms:
This paper is organized as follows. Section 2 discusses related works in VP detection and artificial bee colony (ABC) algorithms. Section 3 states the VP detection problem from a clustering theory perspective. Section 4 details our proposed algorithm, and Sec. 5 presents and discusses the experimental results. The paper concludes with Sec. 6. 2.Related Works2.1.Vanishing Point DetectionFinding the VPs in 2-D perspective projections has received much attention since Barnard’s methodology was proposed in 1983.3 Each line group is often processed by the three elements of line extraction, line classification and VP estimation. Many present studies focus on the second element. With regard to the number of detected VPs, these algorithms aim at estimating three estimate three orthogonal VPs,4,5 or any present nonorthogonal VP.3,6,7 Based on their estimation strategy, line classification algorithms are roughly divided into two categories; algorithms that specify accumulator spaces and those that perform the clustering directly on the image plane. In the former category, an open image plane is mapped into a bounded accumulator space. These algorithms aim for simple operation and do not discriminate between finite and infinite VPs.3,4,8 Each cell in the space accumulates the lines that pass through its corresponding image point. Cells that have accumulated the most lines will produce the candidate VPs. The performances of these algorithms are mainly determined by the selected accumulator space. In the latter category, the workspace is the actual image plane.6,9 Line clustering is generally decided by computations, such as the distances among points and lines. Typical computational methods are random sample consensus (RANSAC) and its variants (such as multi-RANSAC and J-Linkage).7,10–12 These methods iteratively select the minimal sampling set of image features for computing a candidate VP, and retrieve the feature set consistent with that minimal sampling set. Another traditional approach is the EM approach,5,13 which alternates between expectation and maximization steps (denoted as E and M steps, respectively). The E step estimates the line clustering from the given current or hypothesized VPs; the M step computes the VPs using the data clusters estimated in the E step. Although accumulator space–based algorithms require the intrinsic camera parameters, clustering in the image plane operates in an uncalibrated setting. However, RANSAC and its variants do not guarantee an optimal solution, whereas the success of the EM approach depends on the initially estimated VPs. Our present study attempts to overcome the inherent limitations of conventional image plane clustering algorithms, and to detect possible nonorthogonal VPs. 2.2.Artificial Bee ColonyAn ABC algorithm, proposed by Karaboga,14 simulates the intelligent foraging behavior of honey bee swarms. Originally designed for solving multidimensional and multimodal optimization problems, the ABC algorithm has since been extended to other problems. For example, Akay and Karaboga15 concluded that ABC efficiently solves integer programming problems. The ABC variant DisABC, introduced by Kashan et al.,16 was designed for binary optimization. In the ABC algorithm, the possible solutions to the optimization problem are represented as food sources; the nectar amount in each food source indicates the quality (fitness) of the potential solution. A swarm of bees investigates the optimum solution.17–19 Each bee assumes one of the following three roles:
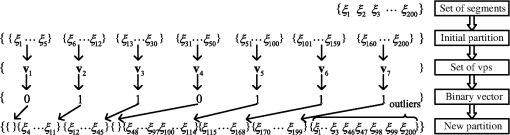
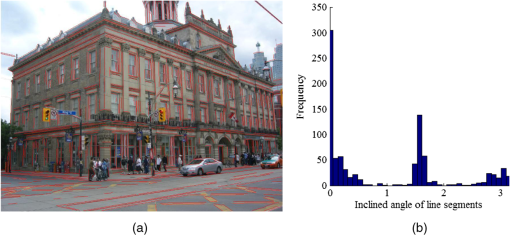
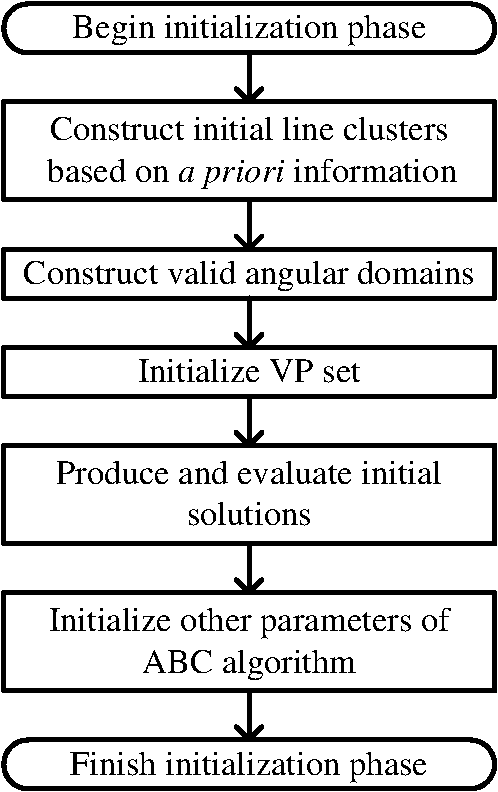
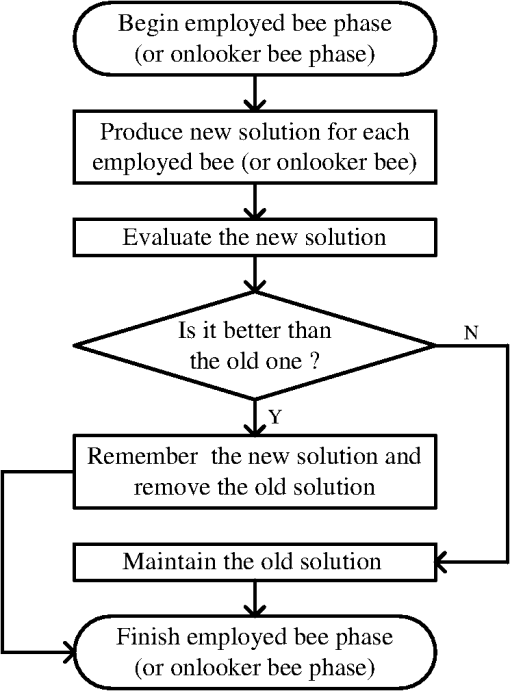
The ABC algorithm randomly creates a set of candidate solutions, and each solution is assigned to one employed bee. It then iteratively executes three important steps to find new solutions. In the first step, each employed bee searches for a new solution within the neighborhood of its current solution. Let be the position of the ’th food source (the ’th solution to the problem), be the dimension of the problem, and be the amount of nectar (quality of the solution). The position of a new food source () is calculated as follows: where is a randomly generated number in the interval and is a randomly generated index with and .If the nectar amount is greater than , the artificial bee memorizes and shares her information with onlooker bees. The position of the ’th food source becomes . If does not exceed , the food source remains at . In the second step, based on the information provided by the employed bees, each onlooker bee probabilistically chooses a candidate solution to further update. The probability is decided by the roulette wheel rule where is the fitness value of the ’th solution, obtained as follows:In the third step, employed bees whose solutions never improve after a predetermined number of trials (called the limit) become scouts and their solutions are abandoned. The scouts embark on random searches for new solutions. The new random position chosen by the scout is calculated as follows: In Eq. (4), and are the lower and upper bounds of the food source position, respectively, in dimension . 3.Problem Statement3.1.Modeling the Problem of Vanishing Point Detection Using Artificial Bee ColonyVP detection is a typical chicken-and-egg problem: if the line clustering is known, then the VPs can be computed reciprocally; if the VPs are known, the line clustering can be retrieved. Therefore, given a set of features describing the linear structure in an image, VP estimation strategies typically proceed by clustering and estimation. The lines are first classified into groups with common VPs. The approximate VP is then located from the line cluster. Like other algorithms, our proposed algorithm alternately iterates the clustering and estimation steps. Especially, the line classification is modeled as an unsupervised clustering problem solved by a novel ABC, and its optimal result is processed by the estimation step. One of the key issues in designing a successful algorithm for VP detection is to suitably assign the line classification solutions to the food sources in the ABC algorithm. In this study, a food source is defined as a binary vector representing a partition of the line set. Binary vector encoding proceeds as follows. Based on some heuristic information, the set of line segments in an image is initially partitioned into line clusters. VPs computed by those line clusters are then collected into a set. A food source is finally encoded as a binary vector whose dimensions are equal to the size of the VP set. Each vector component, either 1 or 0, indicates whether the VP at the corresponding set position is selected to repartition line clusters through the latter optimal steps. As shown in Fig. 1, 200 line segments extracted from an image are initially divided into seven subsets. A VP set is built from each subset producing one VP. A binary vector is randomly generated as a food source (solution) to indicate the selected VP set . The set is then repartitioned so that each line segment is associated with one VP of the set or is marked as an outlier. Another problem that arises when modeling VP detection using the ABC algorithm is how to evaluate and update food sources (solutions).17,18 In the present study, the fitness of a solution is evaluated by validating the line cluster, thus determining whether the cluster is cohesive with low coupling. In particular, a distance function is introduced to measure the deviation between each VP and the corresponding line segment. Moreover, the solutions are updated by the three types of bees (employed bees, onlooker bees, and scouts), as described in Sec. 4. 3.2.A Priori Information of Line SegmentsThe angle of two line segments in an image plane, which corresponds to the perspective view of two parallel lines in an object plane, is related to the shooting angle and the distances between the parallel lines and between the image and the object plane. The shooting angle is usually presented by the angle between the image and the object plane. More specifically, the angle of two segments widens as the shooting angle becomes larger or as the parallel lines become more separated, but decreases with an increasing distance of the two planes. In practice, the distances between parallel lines in a man-made environment are distributed within a certain range, whereas the scene images have often been shot from a general shooting angle at a medium-to-long distance. Therefore, the angle between two arbitrary line segments, corresponding to a family of parallel lines in 3-D space, is constrained within a small interval. Furthermore, we know a priori that parallel lines are often similarly inclined in medium-to-long range scenes. For example, consider the building image in Fig. 2(a). We first compute the inclination angle of each line segment in the image; next, we construct a histogram of the inclined angles [see Fig. 2(b)]. The inclined angles of the line segments clearly concentrate within several subintervals of the histogram. 3.3.Preliminary Processing of the Initial ClusterThe input to our algorithm is a set of line segments , which are obtained from the image () using a line segment detector (LSD). Each line segment is represented by its two endpoints expressed as homogenous coordinates . From the input matrix, we can derive other attributes of such as the length () and inclined angle (). Among the many line segments typically contained in , very short segments contribute little information for the VP detection. Therefore, line segments shorter than 5% of the image height are filtered from set . Sequentially, outliers with anomalous inclined angles are also removed. To initialize the proposed algorithm, the set of remaining line segments is then partitioned into several groups. The preprocessing of set is detailed in the Secs. 3.3.1 and 3.3.2. 3.3.1.Initialize the line clustersBased on the priori information, the line segments are segregated by their inclined angles. The interval of the inclined angle of line segments, , is first divided into several subintervals. The number and scale of a subinterval, denoted as and , respectively, are determined from the real situation. Empirically, we set to 36 and to . Then based on their inclined angles, the line segments are split into subsets called angular domains, denoted as (). In this way, line segments whose inclined angles occupy the same subinterval are collected into the same angular domain. 3.3.2.Initializing the solution vectorsThe number of line segments in each angular domain is denoted (). is marked as an invalid angular domain if equals 0 or 1. If is 1, we check whether the left and right neighborhoods of are both invalid angle domains. If true, the line segment is removed from ; otherwise, it is removed from and placed in the neighborhood containing more line segments than the other neighborhood. We denote the number of valid angular domains as , and renumber each valid angular domain as , where . In each valid angular domain , an initial VP () is determined as the cross-product between the two lines () coincident with two segments (), which are randomly selected from . The VPs of all valid angular domains are collected into a set . Next, SN binary vectors with dimensions corresponding to the set are randomly generated for defining the initial positions of food sources in the ABC algorithm. Each component of each binary vector indicates whether the corresponding VP in is selected as a reference point in the line segment classification. Note that the new positions of the scout bees are also randomly generated by the above initialization procedure. 4.Artificial Bee Colony Algorithm for Vanishing Point Detection4.1.NotationA novel ABC algorithm called DCABC is presented in this section. For this purpose, we first define some essential symbols: is the line passing along segment , represented in homogeneous coordinate form. is the maximum number of line classifications, determined by the number of valid angular domains. is a valid angular domain indexed by with . is a VP initialized by the dth valid angular domain (). is the set of VPs, where is a VP corresponding to . is a line cluster of segments closer to than to any other VP in . is a binary vector of food source positions in the DCABC. If , the corresponding in has been selected as part of the solution proposed by . If , is excluded from the solution. is the position of the best current food source. is a subset of VPs, represented by a position vector , such that with . is the set of VPs in that have not been selected by , such that with . denotes the distance between the VP and the line segment . 4.2.Partition Strategy and Validity IndexEssentially, this paper regards the line classification step in the VP detection as a clustering procedure. The clustering process, which separates the objects into groups, is realized by unsupervised or supervised learning. In unsupervised clustering (also known as dynamic clustering), the number of classes need not be specified in the training data. In supervised clustering, the number of classes must be predetermined. Our algorithm belongs to the former category. 4.2.1.Distance functionIn the DCABC, the position vector () of a food source chooses some VPs as clustering centroids from the set (). The algorithm then assigns each segment to the cluster with the closest pseudocentroid , based on the distance function . We also specify a distance threshold (TH) that assigns a segment to the outliers if the segment is separated by more than TH from all selected VPs. Here, the deviation between a line segment and a VP is measured by the distance function. In a previous measurement method,20 the orientation error was considered as the workspace. Thus, we define the distance [] between a VP () and a segment () as the absolute value of the sine of the angle between a line () coincident with the segment and another line () connecting () to the center point of the segment (). Both lines are defined in homogeneous coordinates as and . The homogeneous coordinates of the two endpoints of are recorded in and , respectively, and , and are computed as follows: In the above definition of the distance function, we adopt the absolute value because we are interested in the relative deviation between the orientations of the two lines, not the sign of this deviation. Moreover, the sine function is a suitable choice because approximately equals when the deviation angle is small. 4.2.2.Line classification and evaluationBased on the distance criterion, the set of line segments can be partitioned into several clusters. The quality of the partitioning can be sufficiently assessed by the compactness and separation measures. High compactness indicates that line segments in the same cluster share a high degree of similarity, while high separation means that line segments occupying different clusters are very dissimilar. The validity index of the clustering is given by Since our model seeks the optimal minimum, the solution () is evaluated by the following equation: 4.3.Generating a New PartitionThe ABC algorithm was initially designed for solving numerical optimization problems, which are continuous problems, and has proven successful at this task. However, the present line classification task is treated as a dynamic clustering problem with binary optimization. To adapt the basic ABC algorithm to dynamic clustering problems, we introduce two changes. First, as mentioned previously, the position () of a food source is represented as a binary vector indicating the selected clustering centroids. Second, when generating a new solution by Eq. (1), we substitute the “−” operator with a dissimilarity measure of the binary vectors. This substitution is inspired from the DisABC algorithm,16 but here we modify both the dissimilarity measure and solution reconstruction to ensure low complexity and fast convergence. Before progressing further, we introduce some new notations. Suppose that and are binary vectors with dimensions. Let be the Hamming distance between and , and specify the number of positions at which the corresponding bits of the two vectors differ. The indices of these positions are recorded inReshaping Eq. (1) as and replacing the “−” operator by the Hamming distance between the two binary vectors, the new position is expressed as where the function rounds the input value to an integer, and is a random number distributed within the interval [0,1]. We also define , and assume that has been determined by Eq. (10).In this work, we construct a new solution vector that equalizes and . In other words, the new vector contains bits whose values differ from those of the corresponding bits in . Therefore, is obtained by flipping bits of from 1 to 0, or from 0 to 1, employing problem-dependent heuristics to instruct the bit selection. Let us recap the problem of VPs detection. As previously mentioned, a position vector indicates the VPs selected from the set , which partition the line segments into line clusters. Obviously, the more line segments in a line cluster, the better the VP estimation. Therefore, the number of line segments in each line cluster can be utilized as a heuristic for generating new solutions. A component of a solution vector corresponds to a line cluster , and the number of line segments in is denoted . Therefore, if component is 0, will be an empty set and will also be 0. We collect the current solution and its neighbor into an index set , and create two additional sets and that record the number of line segments in the line clusters indexed by the elements in SI. Specifically, for each index in SI, if equals 1, is added to the set ; otherwise, is added to the set . The new solution vector can be simply constructed from the obtained , , and . The candidate solution is initialized with a copy of and is computed in three steps: (1) select the bit within for which the number of line segments of the corresponding cluster is minimized in and switch it from 1 to 0; (2) select the bit within for which the number of line segments of the corresponding cluster is minimized in and switch it from 0 to 1; (3) delete the minimal value of and the maximal value of . These three steps are repeated until bits are flipped. 4.4.Estimating a Vanishing Point for Segment ClusteringOnce the line segments have been grouped into line clusters based on their estimated VPs, we refine the related VP locations for each line cluster . To this end, we compute the point in the image plane that minimizes the sum of the distances to the lines sharing a common VP. Using the definition of the distance between a VP and a line segment [Eq. (7)], we estimate the VP of line cluster as In practice, Eq. (13) is solved by a least-squares algorithm. 4.5.Description of the Dynamic Clustering Artificial Bee Colony AlgorithmBased on the above analysis, the DCABC algorithm flow is presented in Fig. 3. The main steps of the algorithm include the following stages.
In Stage 1, certain parameters have to be preset for the DCABC algorithm. Generally, onlooker bees form 50% of the colony, employed bees form 50%, and the number of scout bees is, at most, one for each cycle. Here, the number of onlooker bees is selected to be equal to the number of employed bees so that the algorithm has fewer controlling parameters. According to previous research,21 as the colony size increases, the algorithm produces better results. However, after a sufficient colony size is achieved, any further size increase does not improve the algorithm performance significantly. Here, the colony size is empirically set to 30 at Stage 1. The control parameter “limit” determines the “scout bee” production (see Sec. 2.2). The “limit” value is inversely proportional to the scout production frequency; an increase in the number of scouts encourages exploration, whereas increasing the onlookers on one food source encourages its exploitation. A “limit” value of 60 is considered appropriate in the present study, representing a quarter of the product of the colony size with the dimensions of the problem. Criteria 1 and 2 determine the termination conditions for the two cycles, where both are based on the maximum number of iterations, and two variables (,) serve as the counters. Here, the upper limits of and are empirically set to 3 and 35, respectively. 5.ExperimentsExperiments were conducted on the York Urban database provided by Denis et al.22 This database holds 102 indoor or outdoor images in man-made environments and also provides the camera intrinsic parameters and the VPs computed with hand-detected segments. For each image in the York Urban database, we compiled two distinct line sets. The first line set (Lineset1) was compiled from the database holding the labeled ground-truth lines with few outliers. The second line set (Lineset2) was extracted from the image by a LSD,23 and includes many lines corresponding to non-Manhattan directions. For example, Fig. 7(a) shows an image stored in the York Urban database, and Figs. 7(b) and 7(c) show the Lineset1 and Lineset2 extracted from this image, respectively. Both line sets of each image were processed by the following algorithms. All experiments were implemented in MATLAB®, running on a Core i7 920 Intel CPU. Fig. 7Example of a line set: (a) image from the York Urban database, (b) Lineset1 of the database image, and (c) Lineset2 of the image detected by the line segment detector algorithm.  DCABC: DCABC is used for VP detection. GS: GS, proposed by Barnard (1983),3 assumes a Gaussian sphere as the accumulator space. RANSAC: the algorithm proposed by Pflugfelder (2008),11 using RANSAC algorithm to cluster lines. JL: The JL algorithm, proposed by Tardif (2009),7 clusters lines by a J-Linkage algorithm. EM: The EM algorithm is a more recent line clustering algorithm proposed by Nieto (2011).13 The algorithms were evaluated by two performance indicators. The first indicator is the accuracy of the estimated focal length using the VPs. As is well known, two orthogonal VPs and satisfy where is the image of the absolute conic given by , and is the matrix of intrinsic camera parameters provided by the York Urban database.From the estimated set of VPs, we selected a triplet of VPs (, , ) that minimized the sum of squares of the constraint: . We then estimated the focal length and compared it with that provided in the York Urban database. Specially, each term of the above constraint was set to 0, and three focal lengths were separately solved by Eq. (14). The estimated focal lengths, calculated as the mean of the three focal lengths, are presented in Fig. 8. Figures 8(a) and 8(b) show the cumulative histograms of the focal length errors in Lineset1 and Lineset2, respectively, for each image in the database. Fig. 8Cumulative histograms of the focal length errors in the York Urban database images. A point represents the fraction of the images in the database with focal length error below . (a) Focal length error in Lineset1 and (b) focal length error in Lineset2. 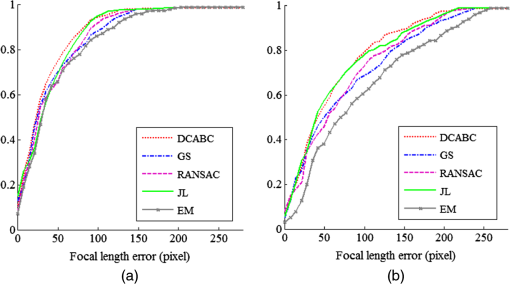 In this test, the five evaluated algorithms demonstrated comparable accuracy performance, although DCABC was slightly more accurate than its four competitors [Fig. 8(a)]. The focal length error of DCABC was less than 78 pixels for 90 out of 102 images in the database, and below 150 pixels for all images. The accuracies of all algorithms, but especially that of EM, decreased when processing Lineset2. Overall, the results were similar to those of the ground-truth lines (Lineset1). Again, DCABC performed slightly better than the other algorithms [see Fig. 8(b)]. The second performance indicator is the computational time of detecting the VP. In this evaluation, we measured the time spent on line clustering and VP estimation, and excluded the line segment detection and selection of the three orthogonal VPs. Figure 9 presents the minimal, average, and maximum computational times required to process both line sets. We observe that EM and DCABC are the fastest and second-fastest of the tested algorithms, respectively. The JL and GS algorithms calculate intersections, which is time-intensive when is large. However, in DCABC and RANSAC, only a small fraction of the intersections are calculated from a few randomly chosen lines. In the EM algorithm, lines are directly clustered with no intersection calculations. Consequently, the EM and DCABC algorithms are time-economical. The mean computation time of DCABC was only 0.023 s for Lineset1 [Fig. 9(a)] and 0.058 s for Lineset2 [Fig. 9(b)]. Fig. 9Computational time of detecting the VPs in the York Urban database images. Algorithms were programmed in MATLAB®. (a) Time of processing Lineset1 and (b) time of processing Lineset2. 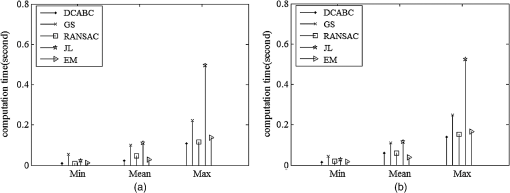 In summary, the five tested algorithms detected the VP with similar accuracy in the lower-noise case. The accuracy of all algorithms declined when some outliers were added. The decline was especially noticed in the EM algorithm. However, EM is the most efficient of the five algorithms, with DCABC a close second. Clearly, our proposed algorithm achieves a good balance between accuracy and efficiency. 6.ConclusionsGiven a set of lines extracted from uncalibrated images, we proposed a means of directly detecting all possible nonorthogonal VPs in the image plane. Treating the task as a dynamic problem of clustering line segments, we partitioned the line clusters by our proposed DCABC algorithm. Initially, the line segments were clustered based on the similarity of their orientations. The clustering was then refined by DCABC using optimization technology in binary space. Finally, a VP was estimated in each of the optimized line clusters. In DCABC, the set of candidate VPs was encoded as a binary vector whose elements indicated the selection status of the corresponding VP. To simplify the new solution construction and accelerate the algorithm convergence, we computed the Hamming distance between two binary vectors and adopted the number of segments in each cluster. Our approach provides a promising bioinspired solution for practical VP detection. AcknowledgmentsThis work was supported partly by the National Natural Science Foundation of China (Nos. 61401195 and 61263029), the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (No. 13KJB520009), and the Key Project of the Young Foundation of Nanjing Institute of Technology, China (Nos. QKJA201204 and QKJA201305). ReferencesA. Minagawa et al.,
“Line clustering with vanishing point and vanishing line,”
in Proc. Int. Conf. on 1999 Image Analysis and Processing,
(1999). Google Scholar
X. Ding et al.,
“Stereo depth estimation under different camera calibration and alignment errors,”
Appl. Opt., 50
(10), 1289
–1301
(2011). http://dx.doi.org/10.1364/AO.50.001289 APOPAI 0003-6935 Google Scholar
S. T. Barnard,
“Interpreting perspective images,”
Artif. Intell., 21
(4), 435
–462
(1983). http://dx.doi.org/10.1016/S0004-3702(83)80021-6 AINTBB 0004-3702 Google Scholar
K. S. Seo, J. H. Lee and H. M. Choi,
“An efficient detection of vanishing points using inverted coordinates image space,”
Pattern Recognit. Lett., 27
(2), 102
–108
(2006). http://dx.doi.org/10.1016/j.patrec.2005.07.011 PRLEDG 0167-8655 Google Scholar
J. Košecká and W. Zhang,
“Video compass,”
in Computer Vision—ECCV 2002,
476
–490
(2002). Google Scholar
F. A. Andaló, G. Taubin and S. Goldenstein,
“Vanishing point detection by segment clustering on the projective space,”
Trends and Topics in Computer Vision, 6554 324
–337 Springer, Berlin Heidelberg
(2012). Google Scholar
J. P. Tardif,
“Non-iterative approach for fast and accurate vanishing point detection,”
in IEEE 12th Int. Conf. on 2009 Computer Vision,
(2009). Google Scholar
B. Li et al.,
“Vanishing point detection using cascaded 1D Hough transform from single images,”
Pattern Recognit. Lett., 33
(1), 1
–8
(2012). http://dx.doi.org/10.1016/j.patrec.2011.09.027 PRLEDG 0167-8655 Google Scholar
A. Almansa, A. Desolneux and S. Vamech,
“Vanishing point detection without any a priori information,”
IEEE Trans. Pattern Anal. Mach. Intell., 25
(4), 502
–507
(2003). http://dx.doi.org/10.1109/TPAMI.2003.1190575 Google Scholar
C. Rother,
“A new approach to vanishing point detection in architectural environments,”
Image Vision Comput., 20
(9), 647
–655
(2002). http://dx.doi.org/10.1016/S0262-8856(02)00054-9 IVCODK 0262-8856 Google Scholar
R. Pflugfelder,
“Self-calibrating cameras in video surveillance,”
University of Reading, UK,
(2008). Google Scholar
M. Kalantari, F. Jung and J. Guedon,
“Precise, automatic and fast method for vanishing point detection,”
Photogramm. Rec., 24
(127), 246
–263
(2009). http://dx.doi.org/10.1111/j.1477-9730.2009.00542.x Google Scholar
M. Nieto and L. Salgado,
“Simultaneous estimation of vanishing points and their converging lines using the EM algorithm,”
Pattern Recognit. Lett., 32
(14), 1691
–1700
(2011). http://dx.doi.org/10.1016/j.patrec.2011.07.018 PRLEDG 0167-8655 Google Scholar
D. Karaboga,
“An idea based on honey bee swarm for numerical optimization,”
(2005). Google Scholar
B. Akay and D. Karaboga,
“Solving integer programming problems by using artificial bee colony algorithm,”
AI(ASTERISK)IA 2009: Emergent Perspectives in Artificial Intelligence, 355
–364 Springer, Berlin, Heidelberg
(2009). Google Scholar
M. H. Kashan, N. Nahavandi and A. H. Kashan,
“DisABC: a new artificial bee colony algorithm for binary optimization,”
Appl. Soft Comput., 12
(1), 342
–352
(2012). http://dx.doi.org/10.1016/j.asoc.2011.08.038 Google Scholar
D. Karaboga and C. Ozturk,
“A novel clustering approach: Artificial Bee Colony (ABC) algorithm,”
Appl. Soft Comput., 11
(1), 652
–657
(2011). http://dx.doi.org/10.1016/j.asoc.2009.12.025 Google Scholar
L. Li et al.,
“A discrete artificial bee colony algorithm for TSP problem,”
Bio-Inspired Computing and Applications, 6840 566
–573 Springer, Berlin, Heidelberg
(2012). Google Scholar
N. Karaboga and M. B. Cetinkaya,
“A novel and efficient algorithm for adaptive filtering: artificial bee colony algorithm,”
Turk. J. Electr. Eng. Comput. Sci., 19
(1), 175
–190
(2011). http://dx.doi.org/10.3906/elk-0912-344 Google Scholar
M. Nieto and L. Salgado,
“Non-linear optimization for robust estimation of vanishing points,”
in 17th IEEE Int. Conf. on 2010 Image Processing (ICIP),
(2010). Google Scholar
D. Karaboga and B. Basturk,
“On the performance of artificial bee colony (ABC) algorithm,”
Appl. Soft Comput., 8
(1), 687
–697
(2008). Google Scholar
P. Denis, J. H. Elder and F. J. Estrada,
“Efficient edge-based methods for estimating Manhattan frames in urban imagery,”
in European Conf. on Computer Vision,
197
–210
(2008). Google Scholar
R. G. Von Gioi et al.,
“LSD: a fast line segment detector with a false detection control,”
IEEE Trans. Pattern Anal. Mach. Intell., 32
(4), 722
–732
(2010). http://dx.doi.org/10.1109/TPAMI.2008.300 ITPIDJ 0162-8828 Google Scholar
BiographyLei Han is a lecturer at the School of Computer Engineering, Nanjing Institute of Technology. He received his BE and ME degrees in computer science and technology from China University of Mining and Technology in 2004 and 2007, respectively. Currently, he is pursuing his PhD at Hohai University, Nanjing, China. His current research interests include image processing, computer vision, and visual measurement. Chenrong Huang is a professor at the School of Computer Engineering, Nanjing Institute of Technology. She received her PhD from Nanjing University of Science and Technology in 2005. Her research interests cover image processing, virtual reality, and computer vision. Tanghuai Fan is a professor at the School of Information Engineering, Nanchang Institute of Technology. He received his PhD from Hohai University in 2010. His research interests cover image processing, telemetry and telecontrol system. Shengnan Zheng received her BS degree in Electronic Information Science and Technology from Nanjing Institute of Technology, in 2006, and MS degree in digital image processing from HoHai University, Nanjing, China, in 2010. From 2010, she held a laboratory technician position in Nanjing Institute of Technology. She is currently pursuing the PhD in hydro informatics from HoHai University. Her current research interests include image processing, image segmentation and analysis, object detection and recognition. |