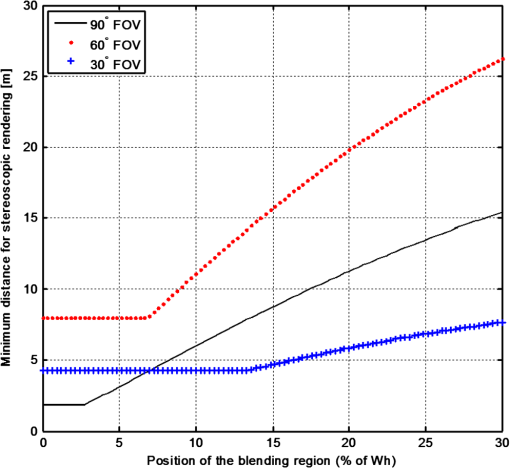
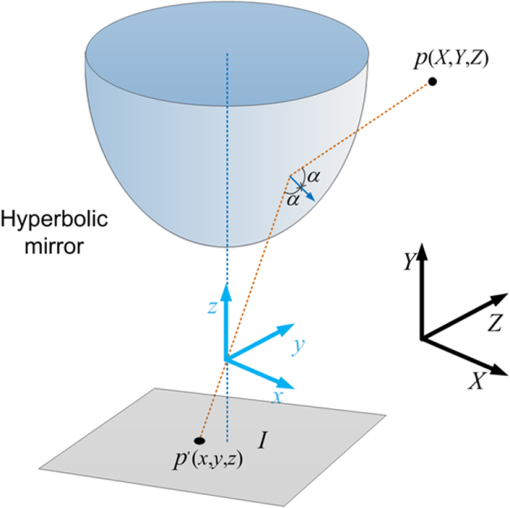
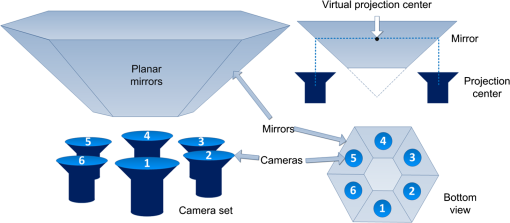
|
|
1.IntroductionIn recent years, the availability of single-snapshot panoramic cameras has enabled a variety of immersive applications. The improved realism attained by using real-world omnidirectional pictures instead of synthetic three-dimensional (3-D) models is evident. However, a camera capable of capturing stereoscopic panoramas of dynamic scenes in a single snapshot is a problem still open for contributions since most of the omnistereoscopic acquisition strategies are constrained to static scenes. Special distinction has to be made between dynamic and static scenes. Most practical scenarios are intrinsically dynamic, and hence a practical omnistereoscopic camera should be able to provide the means to render (in real time or off-line) two views of the scene with horizontal parallax, in any arbitrary gazing direction with respect to the capture viewpoint. These two views must correspond to the views from the left and right eyes of a human viewer since they should be able to stimulate the mechanism of human binocular vision, reproducing a credible and consistent perception of depth. A few cameras can capture omnistereoscopic visual information in a single snapshot, but some of these cameras are unsuitable to produce omnistereoscopic views suitable for human binocular vision, while the capabilities of other potentially suitable cameras have not been formally demonstrated. In order to satisfy the constraints of the problem as defined, we need a panoramic camera capable of acquiring all of the scene’s necessary visual information to reconstruct stereoscopic views in arbitrary directions. The camera must sample the necessary visual information omnidirectionally from a chosen reference viewpoint in space, and it has to do this in a single snapshot to account for scene dynamics. Consequently, sequential acquisition strategies to create stereoscopic panoramas are inadequate for this problem. Despite this, some sequential strategies have inspired multicamera configurations that may be suitable for the task. However promising, the capabilities of these multicamera techniques have not been properly justified by theoretical models of omnistereoscopic image formation. Furthermore, there is a need for a model to represent the binocular and omnidirectional viewing of the scene. Finally, a formal analysis to evaluate the performance of an omnistereoscopic camera taking into account a model for the human binocular vision is still waiting. In 2001, Zhu1 presented an extensive classification of the different technologies to create omnidirectional stereoscopic imagery. This was an excellent survey of omnistereoscopic methods up to its publication date, which presented a taxonomical classification of camera configurations and methods, comparing their capabilities to produce viewable stereoscopic imagery in any azimuthal gazing direction around the viewer. However, the real-time acquisition of dynamic scenes, which is relevant for today’s multimedia applications, was not taken into account in that work. In this paper, we review and classify different panoramic cameras and acquisition strategies available to date to produce realistic stereoscopic renditions of real-world scenes in arbitrary gazing directions. 2.Panoramic Representations for Omnistereoscopic VisionPanoramic images can be represented in any of the omnidirectional image formats, e.g., cylindrical, cubic, spherical, etc. In some cases, the representation can be truly omnidirectional; in other words, the visual information acquired by the camera is projected on a 3-D surface covering 360 deg in azimuth and 180 deg in elevation. These panoramic representations are spherical, or projections of the scene on topological equivalents of a sphere, e.g., cubic or dodecahedral projections to name some. These complete omnidirectional representations are common for monoscopic panoramas where the scene is acquired from a single viewpoint or, at least, an approximation to a single viewpoint, where images are acquired from close but different viewpoints. In the case of stereoscopic panoramas, the scene is generally acquired from two distinct viewpoints with horizontal parallax, for every possible gazing direction in azimuth and for a limited range of gazing directions in elevation. The latter viewing model has a correspondence with the human binocular visual system, where eyes are horizontally displaced from each other, and they are located on a plane parallel to the reference floor. This idea is illustrated in Fig. 1. In this binocular viewing model, the scene is acquired by rotating the head in azimuth around a viewing point and gazing up and down in a limited range of elevation angles (), always maintaining the geometric constraints of the model. This model can be represented in a cylindrical panoramic format, or a surface equivalent to a cylinder, where the elevation angles are limited to a certain range. Note that when trying to apply the binocular model to a full spherical representation, there are intrinsic difficulties in acquiring and rendering stereoscopic views with horizontal parallax for elevation angles close to the poles. For this reason, the methods for omnistereoscopic image acquisition are mainly restricted to cylindrical topologies. Fig. 1Binocular viewing model for omnistereoscopic image acquisition where the region of zero parallax (eyes convergence points) is limited to a spherical section, topologically equivalent to a cylinder.  In this review, we focus on methods to acquire stereoscopic panoramas of dynamic scenes to be represented in a cylindrical format. These omnistereoscopic images can be cubic, cylinders or spherical sections, which can be projected inside a cave automatic virtual environment (CAVE) or in a dome-shaped display to create immersive shared experiences. Alternatively, the omnistereoscopic methods reviewed can provide wide-angle stereoscopic renditions of the scene in desired viewing directions, which can be created using the information acquired by the different cameras. The latter application can be seen in head-mounted devices for visualization of stereoscopic virtual environments. 2.1.Acquisition Models for Monoscopic PanoramasThere are two main models for the acquisition of monoscopic panoramas: a singular viewpoint (SVP) model and a nonsingular viewpoint (non-SVP) model, also known as polycentric panoramic model. Any camera or acquisition technique available to produce monoscopic omnidirectional imagery can be classified into one of these two models. In the SVP acquisition model, for any gazing direction in azimuth (camera’s panning direction), there is a unique projection center that marks a single convergence point for all incident light rays. This model groups the catadioptric cameras used to acquire the whole scene using, for example, a single photosensitive sensor array and a curved mirror. Panoramas created by a rotating camera around its nodal point, or its projection center assuming a pinhole camera model, also satisfy the SVP model. These panoramas are created by acquiring planar images to be mosaicked or by scanning the scene column-wise, i.e., using line-sensor cameras and turning platforms. Examples of SVP acquisition are illustrated in Fig. 2(a) and 2(b). Fig. 2Examples of omnidirectional image acquisition: (a) catadioptric cameras based on parabolic or hyperbolic mirrors produce SVP panoramas,2 (b) rotating a camera about its nodal point to acquire multiple perspective projections with a common projection center also produces SVP panoramas, while (c) rotating an off-centered camera to acquire image patches, around a point different than its nodal point, produces non-SVP panoramas, as well as (d) multi-sensor cameras, such as the Ladybug2 panoramic camera,3 which also produce non-SVP panoramas. 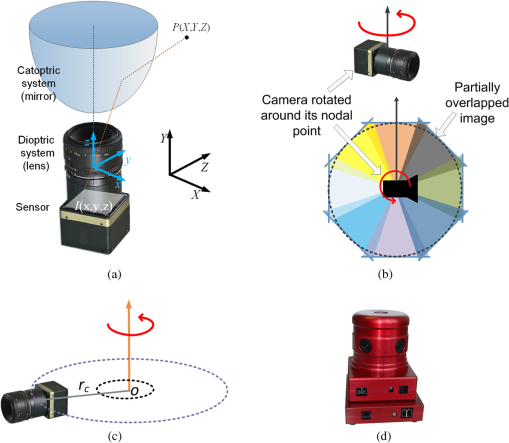 In the case of a non-SVP model, the panoramic image is rendered using a centrally symmetric set of projection centers which are not spatially collocated. Cameras based on the non-SVP paradigm are more common than those based on an SVP model because the physical dimension of multiple camera configurations prevents sampling the scene from a single viewpoint. A way around this problem is using planar mirrors to reposition the projection centers closer to each other, approximating an SVP configuration. In the context of the problem studied in this paper, stereoscopic panoramas are by definition non-SVP panoramas since the scene is imaged from two distinct viewpoints (left- and right-eye viewpoints) for any possible gazing direction. Examples of non-SVP cameras are shown in Fig. 2(c) and 2(d). 2.2.Omnistereoscopic Acquisition ModelsThe different strategies to acquire the necessary visual information to produce stereoscopic panoramas (in a cylindrical format) can be summarized into a limited number of acquisition models. We propose to reduce the classification to four models constrained to acquire stereoscopic panoramic imagery for human viewing. Hence, these models are conceived to represent the acquisition of two images of the same scene from two distinct viewpoints with horizontal parallax. Each of these models represents the stereoscopic acquisition of image pairs for multiple gazing directions in azimuth, and for a limited field of view (FOV) in elevation. All the cameras and acquisition techniques reviewed in this paper can be modeled by one of these four models. The proposed models are suitable to describe the sequential acquisition of visual information toward the rendering of stereoscopic panoramas. A few of the proposed acquisition models are limited to sequential sampling since inherent self-occlusion problems prevent them from being implemented using multiple sensors. But some of the proposed cases can also model the simultaneous scene acquisition, i.e., using multiple sensor configurations or other omnidirectional camera systems. The simultaneous acquisition case is of particular interest in the context of the problem studied in this paper. The first stereoscopic acquisition model is the central stereoscopic rig, which is illustrated in Fig. 3(a). In this case, two coplanar cameras separated by a baseline determine a viewing circle concentric with the geometric center of the camera arrangement. The viewing circle is the virtual circle determined by the trajectory of both cameras while panning all azimuthal angles () around . This model for omnistereoscopic rendering has been widely used in the literature over the last decade to represent a stereoscopic rig panning the scene in azimuth.4 This model is suitable to represent the sequential acquisition of partially overlapped stereoscopic image pairs with respect to a common center.5 In all of the four acquisition models, a single- or dual-camera system samples the scene for different on a plane parallel to the reference floor as illustrated in the binocular viewing model of Fig. 1. Finally, this model can also represent a widely used technique based on extracting two columns, corresponding to the left- and right-eye perspective, from the sequence of planar images acquired using single camera rotated off-center.6,7 However, due to self-occlusion between cameras, this model cannot be applied in a parallel acquisition configuration. Fig. 3Omnistereoscopic acquisition models using multiple-camera configurations: (a) central stereoscopic rig, (b) lateral stereoscopic rig, (c) lateral-radial stereoscopic rig, and (d) off-centered stereoscopic rig. 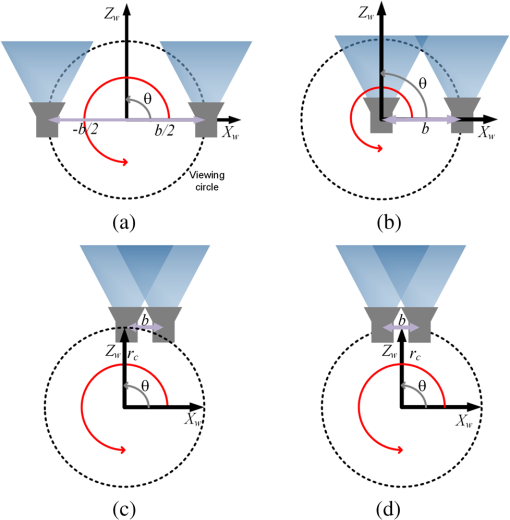 The lateral stereoscopic rig model is shown in Fig. 3(b). This model represents a viewing circle centered at the projection center of one of the two cameras. The off-centered camera (stereoscopic counterpart) describes a circle of radius equal to the stereo baseline while rotating around the center . In this model, one camera is used to produce an SVP panorama centered at (nodal point of the central camera), while the second camera is used to estimate the scene’s depth by acquiring stereoscopic counterparts of the images acquired by the central camera.8–11 This method enables horizontal disparity estimation and the extraction of occlusion information to be used in the rendering. For similar reasons as in the previous acquisition model, this acquisition model cannot be used in a parallel acquisition scheme due to self-occlusion between cameras. The lateral-radial stereoscopic rig model, which is shown in Fig. 3(c), can be derived from the lateral stereoscopic rig model presented above, by adding a radial distance between the symmetry center and the nodal point of one of the cameras (central camera in the previous model). This is a more general model where the nodal points in a multiple-sensor arrangement cannot be concentric due to the physical dimension of each camera.12 The lateral-radial stereoscopic rig model can also represent a stereoscopic rig rotated off-center, where one camera is radially aligned with the center , while the second camera is horizontally displaced to capture another snapshot with horizontal parallax. This model can represent a parallel acquisition scheme, i.e., a multiple-sensor arrangement. The off-centered stereoscopic rig models a stereoscopic rig located at a radial distance from the geometrical center as depicted in Fig. 3(d). This model is suited for camera configurations where multiple cameras, usually a large number of them, are radially located with respect to a center . These cameras, when taken in pairs, define a series of radially distributed stereoscopic rigs. The partially overlapping FOV between even (or odd) cameras can be used to mosaic vertical slices of the scene, rendering a stereoscopic pair of panoramas.13 Multicamera configurations have been proposed14 using () radially distributed stereoscopic rigs. These configurations are based on acquiring a number of partially overlapped stereoscopic images of the scene. This model of acquisition can also represent a parallel acquisition of multiple stereoscopic snapshots of the scene. 2.3.Comparing Different Camera ConfigurationsSeveral omnistereoscopic acquisition and rendering techniques have been proposed over the last decade. Most of them are not suitable for acquiring dynamic scenes omnistereoscopically, but some configurations satisfy this constraint. Unfortunately, the pros and cons of the panoramic cameras suitable for the task are still open to research. In order to understand the limitations of the different camera configurations, we simulated some basic characteristics of the four configurations presented in the previous section. One fundamental aspect to consider is the continuity of the horizontal disparity between partially overlapped stereoscopic snapshots. This is particularly important when the rendering is based on mosaicking. In Fig. 4, we compared the relative variation in the minimum distance to maintain continuity in the horizontal disparity between mosaics. The idea is to find the minimum distance to the scene to have subpixel variations in the horizontal disparity between adjacent image samples. Our simulations were based on an APS-C sensor size () of 10.1 megapixels. The case presented here, which is shown as an example only, corresponds to one particular combination of baseline and lenses’ FOV for the four camera models. The simulation result shows a reduction in the minimum distance for stereoscopic rendering achievable for the all the acquisition models, compared against Model 1, as a function of the blending position in each image. In this particular example, for the camera Models 2 and 3, the relative minimum distance increased more than in other camera models when the blending threshold is above 12% of the image width , measured from the edge of each image to mosaic. Fig. 4The acquisition models are contrasted against the central stereoscopic rig (model 1) showing the relative variation of the minimum distance to the scene to achieve horizontal disparity continuity among neighbor images: the compared configurations are lateral stereoscopic rig (model 2), the lateral-radial stereoscopic rig for (model 3), and the off-centered stereoscopic rig for (model 4).  Also important in the camera design is the minimum distance to the scene to have an object imaged by adjacent stereoscopic sensor pairs; in other words, how far the stereoscopic FOV is located with respect to the panoramic camera. This distance depends on the multiple cameras’ geometric configuration, the FOV of each camera, and the stereoscopic baseline. In another example, we contrasted the minimum distance for stereoscopic rendering using the same baseline and changing the lenses’ FOV only. The results presented in Fig. 5 correspond to the camera Model 1 for a fixed baseline length and three FOV cases. The simulation results show that the minimum acceptable distance to maintain stereoscopic continuity between mosaics as a function of the blending position in each image. As in the previous case, the blending position is expressed as a horizontal length, measured from the edge of the image as a percentage of the image width. 2.4.ProblemThe main problem of the omnistereoscopic image acquisition for human viewing is how to sample the complete visual field at once, from two viewpoints with horizontal parallax. Furthermore, if using multiple cameras to do this, how to avoid the self-occlusion between cameras and how to minimize the problems introduced by sampling the scene from close but different viewpoints. The self-occlusion problem is common to all the conceptualizations of panoramic photography, which must be considered when a single or multiple cameras are used to sample the scene omnidirectionally. If the image sampling is sequential, self-occlusion can be avoided. However, the acquisition of dynamic scenes exacerbates the restrictions since all the information to produce omnistereoscopic images has to be acquired at once. The parallax arising from sampling the scene from different viewpoints is another problem common in panoramic photography. The problem gets more complicated when the simultaneous acquisition of stereoscopic images from different viewpoints enters into the equation. One possible solution to the problem is to acquire multiple stereoscopic snapshots of the scene simultaneously. In this case, the geometric configuration of the multisensor device must be carefully designed to avoid self-occlusion that occurs when one camera lies in the FOV of another. Alternatively, another possible solution is using diffractive optics to obtain two views of the scene with horizontal parallax, and doing so omnidirectionally. In this case, the image formation for this type of diffractive lens has to be modeled and the capabilities of such a camera have to be assessed. A camera under these constraints should be able to acquire an omnidirectional binocular snapshot of the whole scene. The information captured by this camera should be sufficient to render two non-SVP panoramic views corresponding to the left and right eyes or, more generally, for stereoscopic renditions of the scene in any arbitrary gazing direction. 2.5.Panoramic Acquisition: Cameras and MethodsThe omnistereoscopic technologies reviewed in this paper were classified into four families based on their image acquisition strategies and/or their constructive characteristics.
This classification in families is independent of the four models of omnistereoscopic image acquisition presented in Sec. 2.2. Nevertheless, each omnistereoscopic technology representative of these four omnistereoscopic families can be modeled using one of the four acquisition models introduced above. The catadioptric cameras based on vertical parallax are the only exception to this rule, since all the presented acquisition models are based on horizontal stereo. In the following section, the pros and cons of each family are studied individually, distinguishing those cameras whose characteristics can be adapted to an omnistereoscopic configuration suitable for acquiring dynamic scenes. 3.Catadioptric CamerasA catadioptric panoramic camera captures a complete 360 deg in azimuth by combining the use of mirrors (catoptric system) to reflect the light arriving from every direction toward a lens system (dioptric system), which focuses the light over a planar photosensitive sensor. In the case of a parabolic profile mirror, light rays emanating from the mirror’s focal point are reflected outward as parallel rays. Conversely, by applying the principle of reversibility of the optical path, ray paths intersecting the mirror’s inner focal point are reflected parallel to the mirror’s symmetry axis. A dioptric system coaxially located at a certain distance from the mirror surface focuses the light over a planar photosensitive sensor. The principle is analogous to a parabolic dish antenna, which collects electromagnetic radiation at its focal point by concentrating incident wavefronts arriving from a source relatively far from the antenna. One of the first panoramic cameras exploiting this idea is attributed to Rees,15 who proposed, in 1967, to combine a hyperbolic mirror and a TV camera to provide an omnidirectional view of the scene to the operator of a military-armored vehicle. In Fig. 6, a simplified model of the catadioptric principle is illustrated, showing how a ray of light emanating from the scene point is reflected by the catoptric system and focused by the dioptric system onto the point on the image plane. The acquired image is an orthographic projection of the scene, which can then be projected onto a canonical representation used in panoramic imaging, i.e., cylindrical, cubical, spherical, among others, or to extract a partial FOV of the scene in any direction in azimuth. In a real-world scenario, a parabolic mirror profile reflects light in a quasiparallel fashion, affecting the quality of the orthographic projection. In the case of using a hyperbolic mirror profile, light rays directed toward a focal point (located inside the convex mirror’s surface) are reflected toward the other focal point of the hyperbola, where the dioptric system is located. Panoramic cameras based on the catadioptric configuration, where light is focused on a single projection point, correspond to the SVP model. Following the SVP principle, a full spherical panorama can be approximated by using two coaxial catadioptric cameras back-to-back and mosaicking the semi-hemispherical images originating from each camera. This idea was proposed by Nayar16 in 1997. At about the same time, Baker and Nayar proposed a model for catadioptric image formation,17 from which they concluded that only parabolic and hyperbolic mirror profiles satisfy the SVP criteria. Other configurations of catadioptric cameras based on different mirror profiles, i.e., semi-spherical or multifaceted pyramidal mirrors, exhibit multiple focal points, which makes them require multiple cameras. An example of these non-SVP cameras is illustrated in Fig. 7, where the catoptric system uses planar mirrors. These configurations are being used in commercial panoramic cameras to produce monoscopic panoramas.18,19 The camera configurations described so far can only produce monoscopic panoramas when used as a single-snapshot camera. However, catadioptric cameras can be used to produce omnistereoscopic images when used in clusters.20–22 The case of omnistereoscopic images based on a number of monoscopic panoramas is studied in Sec. 5. Along with the development of monoscopic catadioptric cameras, there has been a parallel development of catadioptric omnistereoscopic cameras. The family of the catadioptric cameras for omnistereoscopic imagery is described next. 3.1.Catadioptric Omnistereoscopic CamerasThe development of omnistereoscopic catadioptric cameras has paralleled the development of general (monoscopic) catadioptric sensors. It should be mentioned that omnistereoscopic catadioptric cameras were originally intended for the real-time estimation of depth maps. In other words, these omnistereoscopic approaches were not intended to produce omnistereoscopic imagery for human viewing, but they were motivated by applications such as robot navigation and 3-D scene reconstruction. One important remark is necessary here: the omnistereoscopic cameras based on a catadioptric configuration with vertical parallax presented in this section are not modeled by any of the acquisition models presented in Sec. 2.2 since the omnistereoscopic acquisition classification has been constrained to human-viewable omnistereoscopic imagery, i.e., binocular stereo with horizontal parallax. One of the earlier examples of this technology was an SVP catadioptric camera proposed by Southwell et al.23 in 1996. This omnistereoscopic catadioptric camera is based on a coaxial, dual-lobe parabolic mirror, and its main application was to generate omnidirectional depth maps of the terrain. A depiction of this camera appears in Fig. 8(a). Fig. 8Omnistereoscopic catadioptric examples: (a) the camera proposed by Southwell et al.23 in 1996 using dual-lobe mirror and (b) an early SVP catadioptric omnistereoscopic camera proposed by Gluckman24 in 1998: this configuration uses two coaxial catadioptric panoramic cameras with a large vertical baseline to acquire two panoramic views of the scene with vertical parallax ; the 3-D scene structure is estimated from the vertical disparity arising between matched feature points in each panorama.  Another configuration was proposed by Gluckman et al.24 in 1998. Their configuration is based on using two coaxial catadioptric cameras whose vertical baseline helps to acquire an omnistereoscopic pair of images. This camera, illustrated in Fig. 8(b), enables the estimation of the 3-D location of a scene point in space, matching pairs of feature points in the panoramic views from each camera. The larger the vertical baseline used, the better the accuracy of depth estimation achieved. A theoretical model of the image formation in a dual-mirror, axially symmetrical, catadioptric sensor was proposed by Stürzl et al.25 The coaxial catadioptric camera has been a popular method to estimate omnidirectional depth over the past two decades due to its simplicity and hardware economy. Unfortunately, it is not suitable to produce a satisfactory omnistereoscopic rendition of the scene capable to stimulate human stereopsis. The binocular visual process is based on fusing two views of the scene obtained from horizontally displaced viewpoints (horizontal parallax). This camera provides two views of the scene in every direction, but based on vertical parallax. Although the omnidirectional depth can be estimated using this information, it cannot be used to produce satisfactory horizontal stereoscopic views. For instance, when using a two-dimensional (2-D) to 3-D conversion, the gaps in image coming from occluded areas need to be filled, e.g., using texture synthesis.26 One of the problems of the vertically coaxial method is that the visual information regarding occluded areas is not acquired. A similar omnistereoscopic camera based on the catadioptric principle was proposed by Kawanishi et al.27 in 1998. Their camera consists of two non-SVP catadioptric cameras in vertical coaxial configuration as shown in Fig. 9(a). Each catadioptric camera consists of six planar mirrors, each of which reflects a partial view of the scene over a video camera. This configuration produces 12 video streams covering 360 deg in azimuth. Each camera in the top of the arrangement is paired with the camera located directly below, i.e., the cameras and form a stereoscopic camera pair, whose vertical baseline is , as illustrated in Fig. 9(b). Similar to Gluckman’s camera,24 the vertical parallax between camera pairs enables the panoramic estimation of the scene’s depth but does not provide the means to render viewable stereoscopic images. In a follow-up of this design, Shimamura et al.28 built a working prototype based on the Kawanishi et al. design capable of producing panoramic depth maps. Fig. 9Omnistereoscopic camera configuration based on coaxial planar mirrors: (a) configuration based on Kawanishi et al.’s idea27 and (b) virtual location of each camera’s projection center and vertical baseline .  Spacek29 relaxed the non-SVP condition using two conic mirrors, instead of pyramidal mirrors, coaxially aligned with cameras. This configuration was conceived to estimate distances based on vertical disparities. The author reported benefits over other profiles in using conical mirrors in terms of the uniformity of the resolution density. However, this type of profile introduces out-of-focus blurring in some regions of the orthographic image because the optical focus is not uniformly located as in the case of hyperbolic and parabolic mirrors. A recent interesting development is due to researchers at the Fraunhofer Heinrich Hertz Institute,30 who are currently working on a prototype of an omnistereoscopic high-definition television (HDTV) camera based on a catadioptric design. Conceived for omnistereoscopic 3-D TV broadcasting, this setup uses six stereoscopic camera rigs, each of which is associated with a planar mirror. Each mirror reflects a partial view of the scene on a camera pair, for a total of 12 HDTV cameras.31,32 These video streams can be mosaicked into a full omnistereoscopic video, or into free-panning 3-D TV signal. The concept of this camera is presented in Fig. 10. The creators of this camera have reported difficulties when mosaicking partially overlapping stereoscopic frames due to the large parallax between adjacent projection centers.33 Part of the problem resides, as in other star-like configurations, in the excessive parallax introduced by the stereoscopic rigs where both cameras are laterally displaced with respect to each other. The minimum distance to objects in the scene for correct rendering is affected by the large intercamera parallax, reducing the stereoscopic usability in foreground regions of the scene. This camera configuration can be represented by the off-centered stereoscopic rig acquisition model [Fig. 3(d)], where six stereoscopic camera rigs, equally distributed at a distance from the geometric center , simultaneously capture six partially overlapped, stereoscopic video signals of the scene. Fig. 10Omnistereoscopic video camera developed at the Fraunhofer Heinrich-Hertz Institute: (a) each planar mirror face is associated with a stereoscopic pair of cameras, (b) locations the cameras as seen reflected on the planar mirrors. 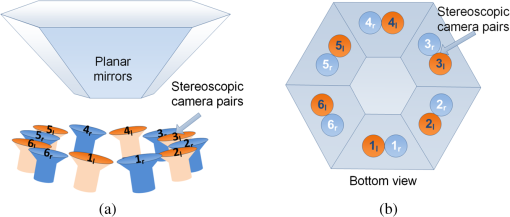 Peleg et al.34 proposed a different catadioptric camera configuration capable of acquiring horizontal binocular stereo omnidirectionally and in real time. This catadioptric system uses a complex spiral lenticular lens and an optical prism to acquire a complete omnistereoscopic image in real time. This configuration deflects incoming light rays as if the scene were acquired simultaneously from multiple perspective points located on a virtual viewing circle (Sec. 2.2). This camera can be modeled by the central stereoscopic rig acquisition model [Fig. 3(a)], where a large number of stereoscopic image vertical stripes (central columns of left and right images) are simultaneously sampled and mosaicked to create complete left and right cylindrical panoramas in real time. The proposed lenticular arrangement is shown in Fig. 11(a), which illustrates the acquisition of a one eye (left or right) panoramic view. The idea of using a Fresnel-like diffractive system with thousands of lenses to capture both omnistereoscopic views simultaneously could, in theory, produce an omnistereoscopic video in real time. The lenticular arrangement can be built around an SVP panoramic camera as shown in Fig. 11(b). The authors have proposed using a beam splitter and the described lenticular system to acquire both viewpoints of a stereo projection simultaneously as illustrated in Fig. 11(c). Fig. 11Peleg et al.’s34 proposal for a real-time omnistereoscopic camera based on a catadioptric principle: (a) a Fresnel-like lenticular lens arrangement diffracts the light over a viewing circle, (b) a catadioptric scheme with a cylindrical diffractive material composed of vertical stripes of the proposed Fresnel lens to capture one (left- or right-view) panorama, and (c) using an optical beam splitter, e.g., a prism, and combining diffraction lenses for left and right view in the same cylindrical surface, both (left- and right-eye) views can be captured simultaneously. 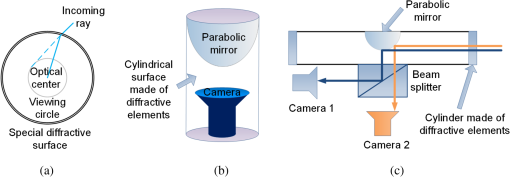 This camera could be a solution to the problem of omnistereoscopic image acquisition of dynamic scenes. Furthermore, Peleg, Ben-Ezra, and Pritch were granted a patent35 for this camera in 2004, but no prototype has yet been built or licensed to the best of our knowledge. This commercialization lag must not be taken as a proof of the inadequacy of the idea; e.g., more than 70,000 patents were granted annually in the United States by the turn of the century and only a very few of them were commercially developed.36 As a matter of fact, a variation of the lenticular lens, although not an omnistereoscopic application, has been licensed for the production of 3-D billboards.37 Peleg et al. proposed a geometrical model of their elliptic lens;38 however, there still are aspects of the image formation for this camera that have not been extensively studied. More importantly, the capabilities of such an optical approach to produce high-quality omnistereoscopic imagery has not been demonstrated. It is important to remark that a cylindrical stereoscopic panorama produces a correct binocular experience only in the center of each rectangular view extracted from these left and right panoramas. The peripheral image region, outside the image center, produces a distorted binocular perception. This effect was mentioned by Bourke39,40 while addressing the problem of semi-spherical omnistereo to display in dome surfaces. Although this is a noticeable effect, the user tends to focus on a region of interest (ROI) at the center of the image, where the binocular perception is correct, reducing the likelihood of uncomfortable effects that could lead to eye strain. Furthermore, if a cylindrical omnistereoscopic image created with this acquisition method was projected in a cylindrical surface around the user (located at the center), a correct binocular depth would be experienced by looking in any direction around the user, as long as the zero parallax distance (eyes vergence) coincides with the distance to the cylindrical screen.41 Other configurations based on catadioptric cameras that appeared in the last decade mainly focused on the problem of omnidirectional stereo reconstruction42,43 following the idea of coaxial catadioptric stereo, which makes them inadequate to produce omnistereoscopic imagery suitable for binocular human viewing. 3.2.Pros and Cons of the Catadioptric Omnistereoscopic CamerasThe most evident advantage of an SVP catadioptric camera is its simplicity: a single camera and dioptric system can sample the scene’s visual field, in addition to estimating the panoramic depth, in a single snapshot. The SVP approach avoids stitching problems and imperfections that arise by parallax between multiple projection centers in non-SVP cameras. However, focusing the light uniformly on a planar image sensor after reflecting light in a nonplanar mirror is problematic. Not all the rays are parallel after reflection in a parabolic surface, nor are they perfectly reflected toward the convex focal point in a hyperbolic mirror. In practice, image blurring as a function of the radial distance from the center of the image17 is difficult to avoid. This problem can be reduced, although not completely, by a careful design of the catoptric system (mirror) and its dioptric (focusing) counterpart. The high-resolution CCD sensors available nowadays can help to reduce problems while resampling the acquired orthographic projection of the scene into a canonical panoramic surface. Furthermore, a catadioptric camera has advantages with respect to other mirror-less systems in terms of reducing chromatic aberrations present in most aspheric lenses, i.e., fisheye lenses. Offsetting the advantages of catadioptric cameras, there are still inherent problems in using this camera to render an omnistereoscopic scene for binocular viewing. Although catadioptric omnistereoscopic configurations using vertically coaxial mirrors are undoubtedly an elegant method for acquiring omnidirectional depth maps in real time, the camera configurations are unable to handle occlusions in the scene. A binocularly correct stereoscopic view can be synthesized with one panoramic image plus a dense horizontal disparity information of the scene. The disparity information can be used to generate a pixel-wise horizontal displacement map. Applying this map to horizontally displace pixels (or regions) in the image can produce a correct illusion of depth. The necessary information to produce this omnistereoscopic image can be acquired using an omnistereoscopic catadioptric configuration: a correct panorama of the scene and an omnidirectional depth map. Unfortunately, the information to fill image gaps (occluded areas) cannot directly be obtained using a camera configuration based only on vertical parallax. But, there are still suboptimal solutions coming from the field of 2-D to 3-D conversion that can be applied. For instance, pixels can be copied from the adjacent regions of the missing areas to fill these gaps. A much better alternative will be to simultaneously acquire a different view, e.g., a horizontal stereoscopic pair for each gazing direction. The parallax view information can be used to fill-in the occluded areas using a texture inpainting technique.44 A good candidate to produce directly viewable omnistereoscopic imagery, capable of satisfing the real-time acquisition of dynamic events as well, is the optical diffractive approach proposed by Peleg et al.,35,45 as illustrated in Fig. 11. However, the design and implementation of such a lenticular arrangement is challenging. Similar to Peleg’s approach, there has been at least one other recent proposal, which is also based on lenticular arrays to multiplex two horizontal binocular views of the scene, but using non-SVP configurations,46 which will be presented in Sec. 6. Besides the lack of commercial interest for an optical-based approach, an alternative solution, based on off-the-shelf lenses and camera sensors, can provide a satisfactory solution to the problem with reduced hardware complexity. Another good candidate is the panoramic 3-D TV camera developed at the Fraunhofer Heinrich-Hertz Institute. This omnistereoscopic camera, which is illustrated in Fig. 10, uses multiple off-the-shelf HDTV cameras and mirrors to produce real-time stereoscopic videos with broadcasting quality. The downfall of this camera is its size31 which makes difficult the mosaicking of individual video streams. One possible solution for the parallax problem would be reducing the size of the cameras, e.g., using custom-made HDTV cameras. Additional improvement may be achieved by using a different camera distribution to enable registering stereoscopic images of scene elements closer to the camera. 4.Sequential Acquisition MethodsA literature review of omnistereoscopic methods and configurations cannot be complete without mentioning the family of sequential acquisition methods. It is necessary to point out that sequential methods are intrinsically inadequate to acquire dynamic scenes omnistereoscopically since they require the scene to be static for correct rendering. However, many multiple-camera configurations that will be presented in Sec. 6 can be directly traced back to parallelized (simultaneous acquisition) versions of sequential methods presented in this section. Therefore, these sequential techniques deserve a closer look. The sequential acquisition of images has been widely used to produce high-quality panoramas. The idea is quite simple: using a single camera, it is possible to capture partially overlapped snapshots of the scene, or image columns, which can be mosaicked to produce panoramas. The simplest approach is a single camera or line sensor rotated around a center , which preferably should be the camera’s nodal point, and taking snapshots of the scene during its trajectory. One example of this method to produce monoscopic panoramas was the Roundshot VR22047 film camera by the Swiss company Seitz Phototechnik AG, which currently offers a line of rotating heads for panoramic acquisition.48 Rotating a single camera around its nodal point can produce SVP monoscopic panoramas only; however, by rotating an off-centered camera, omnistereoscopic images can be created.7 In terms of sequential omnistereoscopic acquisition, the rotating stereoscopic rig models, which are depicted in Fig. 2(a) and 2(b), produce non-SVP panoramas, but they cannot be adapted for a simultaneous acquisition due to self-occlusion between cameras. The acquisition models presented in Fig. 2(c) and 2(d) can be used for sequential or simultaneous acquisition. To produce omnistereoscopic imagery, one of the first sequential approaches has been to rotate a stereoscopic camera rig around the midpoint between nodal points. This corresponds to the central stereoscopic rig model [Fig. 3(a)]. A valid rendering strategy in this case is mosaicking vertical image stripes from the center of each image pair to create left- and right-eye panoramic views. The number of stereoscopic images to be sampled determines the incremental panning angle and the strip width. As was mentioned in Sec. 3.1, the stereoscopic panoramas are correct only at the center of each view, becoming distorted outside the central region. Note that each camera’s projection center (nodal point) defines a viewing circle of diameter during the scene panning. Alternatively, rotating the stereoscopic rig about one camera’s nodal point corresponds to the lateral stereoscopic rig acquisition model [Fig. 3(b)]. Unfortunately, the latter strategy cannot be implemented using multiple cameras for a simultaneous (parallel) acquisition. The other sequential acquisition strategy corresponds to the off-centered stereoscopic rig acquisition model [Fig. 3(d)]. In this case, the scene is sampled by acquiring a sequence of stereoscopic snapshots, rotating the stereoscopic rig off-center with a radius . A modified version of this sequential method consists of radially aligning the nodal point of one of the cameras with the center , which corresponds to the lateral-radial stereoscopic rig acquisition model [Fig. 3(c)]. Both sequential variants can be parallelized for simultaneous acquisition using multiple cameras. The last sequential strategy to acquire omnistereoscopic imagery is rotating a single camera off-center, at a radial distance from the rotation center . This strategy corresponds to the first acquisition model [Fig. 3(a)], where left and right views are acquired during the circular trajectory of the camera by back-projecting vertical image stripes. The image columns’ position relative to the image center can be located by tracing the rays connecting the camera projection center with the points on the viewing circle. There have been attempts to parallelize this sequential acquisition strategy using multiple cameras in a circular radial configuration. These sequential techniques, their variations, and other alternatives are individually detailed in the next section. 4.1.Omnistereo Based on Sequential Acquisition ModelsPerhaps one of the most illustrious applications of omnistereoscopic sequential acquisition was integrated to the Mars Pathfinder rover4 in the late 1990s. The camera can be modeled by the central stereoscopic rig method illustrated in Fig. 3(a). It was designed to provide a variety of telemetric measurements beyond producing omnistereoscopic imagery; actually, producing stereoscopic images suitable for human stereopsis was not the primary goal of this camera. Two cameras were mounted on a retractable mast and were rotated around the midpoint between each camera’s nodal point. The pair of cameras, whose resolution was modest as is expected for an interplanetary probe of that era (), were toed in 0.03 rad, defining a fixation point (zero parallax distance) at 2.5 m from the rotation center. The stereoscopic panoramas produced by this camera received much attention in the news.49–51 Although these omnistereoscopic images are not impressive in terms of quality of the binocular stereo, they constitute an important precedent for the marketing value of realistic immersive imagery to promote a planetary mission to the layperson.52 Other authors reported variations on the rotating stereoscopic rig method that are worth mentioning. For instance, Romain et al.53 proposed a rotating platform with two degrees of freedom, which can rotate in azimuth and elevation to produce spherical omnistereoscopic images. More recently, Ainsworth et al.54 revisited the method of a rotating stereoscopic rig to minimize (not to eliminate as the authors stated) stitching problems. They reported their method to create stereoscopic panoramas55 based on mosaicking partially overlapped scene's images, which they tested using an off-the-shelf digital camera (Panasonic Lumix) and a commercial rotating platform (GigaPan EPIC Pro Robotic Controller). Huang et al.8 proposed a rotating camera to acquire stereoscopic images of scenes, which were aligned and mosaicked to render omnistereoscopic images. Their idea, originally published in 1996, is illustrated in Fig. 12(a), which shows a central camera that is rotated around its nodal point and a second camera that is rotated off-axis, providing a parallax view of the scene. Their method corresponds to the lateral stereoscopic rig model [Fig. 3(b)], which produces non-SVP stereoscopic panoramas, where the stereo budget can be selected by choosing the baseline of the rotating stereo rig. An interesting idea is to acquire stereoscopic images of the scene using a rotating stereoscopic rig, where one camera (central) is in the optimum position to minimize stitching errors (nodal point), while the second camera captures a second view of the scene with horizontal parallax. The central camera produces an SVP panorama while the second camera can be used to render a binocular polycentric panorama. Because of camera self-occlusion, this idea is difficult to implement using multiple cameras, although a multicamera configuration using planar mirrors can approximate an SVP for a central camera and acquire a horizontal parallax view simultaneously. There have not been proposals based on this catadioptric design to our best knowledge. Fig. 12Omnistereoscopic methods based on sequential acquisition of partially overlapped images: (a) method proposed by Huang et al. in 1996 to generate a correct panorama (central camera) and accessory information to estimate a horizontally parallax view (lateral camera) and (b) the acquisition strategy proposed by Yamada et al., which is similar to Huang’s method, is based on acquiring images to produce an SVP panorama (central camera) and, in this case, estimating the panoramic depth map based on a large-baseline stereoscopic pair of images (left and right cameras). 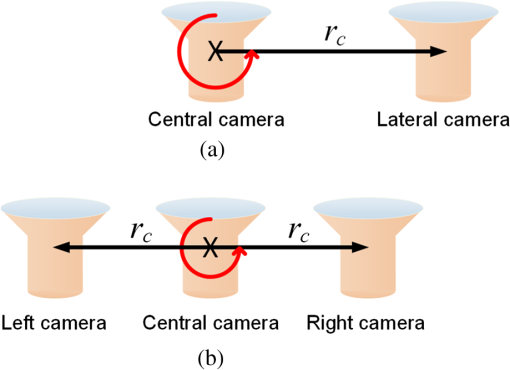 Using a similar approach, Yamada et al.9–11 proposed the triple camera system shown in Fig. 12(b). Similar to Huang et al.’s method, the central camera produces an SVP panorama while the two satellite cameras help to estimate a panoramic disparity map using a large baseline. This sequential acquisition technique can be seen as a modification of the central stereoscopic rig [Fig. 3(a)], used only to estimate depth by exploiting the larger baseline () between the satellite cameras, and adding a central camera to produce an SVP panorama as in the lateral stereoscopic rig model. Again, self-occlusion between cameras makes it difficult to parallelize Yamada’s approach in a simultaneous acquisition scheme. But a catadioptric scheme to acquire an SVP and a multisensor scheme to simultaneously acquire a number of partially overlapped stereoscopic snapshots of the scene is an interesting design challenge and a suitable approach for dynamic scene omnistereoscopic acquisition. No camera following the suggested approach has been proposed to our best knowledge. A variation of the idea of rotating sensors was proposed by Chan and Clarke56 who devised a camera where a mirror is rotated while a single sensor sequentially captures binocular stereoscopic images of the scene. Their idea was inspired from endoscopic applications where a single probe has to be inserted in a biological cavity or in an archeological site. The principle behind the idea is similar to other proposals in terms of a sequential acquisition. For instance, carefully selecting the planar mirror and camera locations, the central stereoscopic rig acquisition scheme of Fig. 3(a) can be implemented with this technique. Ishiguro et al.6 proposed in 1992 a method to create omnistereoscopic imagery based on a single rotating camera, but for robot navigation instead of human visualization. This method corresponds to the central stereoscopic rig acquisition model illustrated in Fig. 3(a). Peleg and Ben-Enzra7 rediscovered this method in the late 1990s, but tailored the idea with human visualization in mind. This method has become one of the most popular sequential techniques to create high-quality omnistereoscopic imagery given its hardware economy and simplicity. The principle is based on a single camera rotating around a point behind its projection center, as depicted in Fig. 13(a). In one complete rotation, the camera captures a number of images that are used to extract left () and right () columns. These two image columns correspond to the back-projection of the image’s vertical stripes defined by intersecting the rays passing through the camera projection center and the points and . The ray tracing concept is depicted in Fig. 13(b). These columns are then mosaicked producing left- and right-eye panoramic views. The end result is equivalent to the central stereoscopic rig model [Fig. 3(a)], used to acquire left and right views column-wise. There have been proposals for omnistereoscopic cameras that can be directly traced to parallelization of a single rotating camera.57,58,59 Fig. 13Rotating method to produce omnistereoscopic imagery based on a single rotating camera: (a) a single camera is rotated from an off-centered location and (b) two projections corresponding to left- and right-eye projections can be defined intersecting the rays passing through the camera’s projection center and the points and defined over a virtual viewing circle. 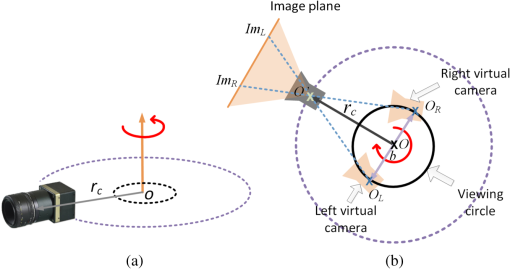 The method has the advantage of defining a virtual baseline that can be varied according to the stereoscopic budget desired for the scene by changing the relative distance between left- and right-eye vertical stripes extracted from the successively acquired images.60 Changing the distance has the effect of changing the viewing circle diameter. More recently, Wang et al. proposed an interactive method to adjust the disparity in panoramas created using the single off-centered rotating camera61 based on the interactive selection of objects in the scene. Examples of 3-D (not stereoscopic) images created using the central stereoscopic rig method for monoscopic panoramas and omnistereoscopic images can be visited online.62,63 Additionally, several patents have been granted to Peleg et al. for acquiring, disparity adjusting, and displaying stereoscopic panoramas using the single-camera method,64–66 one of which has been licensed to HumanEyes,37 not to create omnistereoscopic imagery but to create multiview 3-D billboards. A different approach was proposed by Hongfei et al.5 who used a single digital single-lens reflex camera to successively acquire 12 images of a static scene. First, three stereoscopic image pairs (six images in cd by placing the camera in the positions labeled and [for ] as indicated in Fig. 14(a). After that, the camera is rotated 180 deg and six new stereoscopic images are successively acquired following the pattern illustrated in Fig. 14(b). This acquisition scheme corresponds to the central stereoscopic rig model illustrated in Fig 3(a). Although Hongfei et al.’s method is not suitable for dynamic scenes, a parallelized version of the same idea was already proposed by Baker et al.14 as a patent application in 2003. Fig. 14Method based on rotating a single camera to capture six stereoscopic images by positioning the camera in 12 different locations and orientations: (a) first, the stereoscopic pairs are acquired one-by-one rotating and positioning the camera to the corresponding locations. (b) Finally, the camera is rotated 180 deg around its nodal point and the pairs are sequentially acquired. 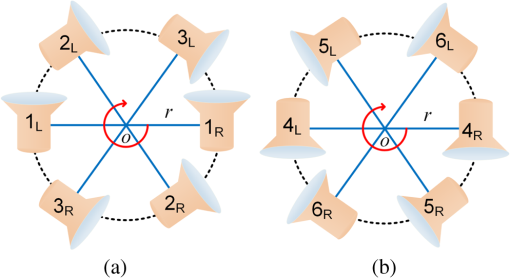 Among the panoramic sequential methods, those based on using line-sensor cameras deserve a particular mention. Cylindrical omnistereoscopic imagery obtained by this method produces geometrically correct binocular views of the scene at the center of the image, while the depth perception is distorted in the periphery of the image.67 This viewing paradigm is valid for cylindrical panoramas projected in a cylindrical display, in both monoscopic and stereoscopic panoramas, in part because it does not have to deal with parallax ghosting while blending images. Sequential line scanning is based on mosaicking image columns a single pixel wide and therefore it produces high-quality stereoscopic panoramas. However, this virtue is offset by their lengthy acquisition time, which is common to all sequential-scanning methods. The line-scanning methods to acquire omnistereoscopic imagery can be modeled by the central stereoscopic rig acquisition method [Fig. 3(a)]. High-quality omnistereoscopic images, in cylindrical format, can be produced using line-scanning sensors. This sequential method has been studied over the first decade of the 2000s,68 thanks, in part, to the commercial availability of line-scanning cameras.69 As their name indicates, these cameras acquire the scene column-wise. An omnistereoscopic view of the scene can be acquired by rotating the line-scanning sensor off-center at radius to acquire independently left () and right () cylindrical panoramas column-by-column. The acquisition model corresponds to the central stereoscopic rig method illustrated in Fig. 3(a), where a line-scanning sensor is in the position of each of the cameras for one complete rotation, acquiring successively each eye viewpoint after two complete rotations. Several authors have contributed to the understanding and modeling of omnistereoscopic imagery using line sensors, covering the line-scanning camera calibration,68,70 a geometrical model for polycentric panoramas using this acquisition strategy,71 and the omnistereoscopic image acquisition.72,73–75 Although the literature on line sensors is extensive and insightful, this approach cannot be adapted to acquire dynamic scenes. Hybrid approaches have been proposed that use a laser range finder and rotating sensors to provide a high-resolution depth mapping of the scene. For instance, Jiang and Lu76 proposed a method that combines an off-center CCD camera with a laser range sensor, which together produced a monoscopic panorama and its dense depth map. Their approach is shown in Fig. 15. Once again, the problem addressed was the reconstruction of a 3-D scene and not the production of a binocular omnistereoscopic imagery. Besides its sequential conception, this idea cannot be used for an omnistereoscopic 2-D to 3-D conversion since occlusion information is not collected during the sequential acquisition. Similar limitations in handling occlusions arise in a recent proposal by Barnes,77 which combines ground-based LIDAR and monoscopic panoramas. Fig. 15Combined camera and laser range sensor in a rotating platform for sequential acquisition: an SVP panorama plus a panoramic depth map can be obtained for static scenes using this acquisition method.76 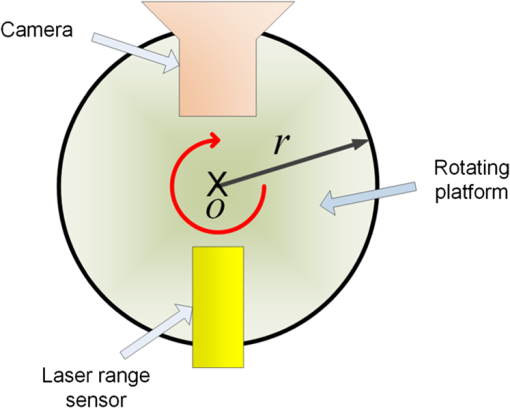 The rotating sensor for omnistereoscopic imagery has appeared with some variations over the last decade.67,78 A good summary of methods to create omnistereoscopic images based on rotating sensors was published in 2006 by Burke.79 4.2.Pros and Cons of the Sequential AcquisitionSequential acquisition strategies are an interesting starting point to devise multicamera configurations for real-time omnistereoscopic acquisition. The configuration proposed by Huang and Hung8 is interesting since it presents a solution to reduce the parallax-induced errors while stitching multiple images. This method can be parallelized to simultaneously acquire a number of image patches and their corresponding stereoscopic counterparts in a non-SVP scheme. The sequential method of Peleg and Ben-Enzra using a single off-centered camera7 is interesting for reducing the hardware involved, but it is difficult to parallelize since it would require a prohibitively large number of cameras to prevent blending artifacts while mosaicking. In that case, the mosaicked image columns have to be constrained to a few pixels wide, which implies taking hundreds of snapshots. A multiple-camera configuration that attempts to take this number of simultaneous pictures is impractical, but, as will be shown in Sec. 6, some multiple-camera configurations that do this parallel acquisition have been proposed. The large overhead when acquiring hundreds of snapshots to just use two narrow slices is partially compensated by line cameras, which scan the scene column-wise. Unfortunately, the large acquisition time of line cameras limits them to controlled static environments, e.g., mostly indoor scenarios. However, it is possible to devise improvements in acquisition speed of omnistereoscopic images using line sensors. For instance, using multiple stereoscopic line sensors, the acquisition speed can be increased linearly with the number of stereoscopic sets. This approach would enable the simultaneous capture of nonoverlapping stereoscopic images of the scene, which can then be mosaicked to create a full omnistereoscopic image in a fraction of time that a single sensor can achieve. Unfortunately, a rotating camera system with such characteristics is still commercially unavailable and, if it were available, it would not be suitable to acquire dynamic scenes. 5.Omnistereo Based on Panoramic SourcesThe panoramic-based methods use panoramic snapshots as raw material to synthesize omnistereoscopic images of a scene. This is a relatively new alternative resulting from the commercial availability of panoramic cameras during the last decade, which made capturing panoramic snapshots of the scene practical. The idea of using multiple stereoscopic panoramas of the scene to perform a 3-D mapping of a scene had started in the late 1980s.80 For instance, Ishiguro et al.6 proposed to render a sequence of omnistereoscopic images, not for human viewing but to estimate the 3-D relationship within objects in a scene. To do this, the authors proposed to use a mobile platform (a robot) equipped with a rotating camera mounted on top. The mobile unit moved on a preprogrammed route, stopping at intervals to acquire omnistereoscopic images of the scene using the single rotating sensor. The central stereoscopic rig acquisition model was used. This sequence of omnistereoscopic views can be used to estimate the distance to obstacles from the traveling path by matching feature points between stereoscopic images obtained between successive panoramic views, e.g., exploiting motion parallax between samples. This method is constrained to static scenes, the panoramas have to be coplanar, the location of each panoramic sample has to be precisely known, and, more importantly, the accuracy of the estimation decreases as soon as the viewing direction approximates the direction of motion progression (robot acquisition path). The panoramas can be aligned by determining the cylindrical epipoles or, alternatively, by finding the focus of expansion81 direction using motion analysis between panoramic frames in the sequence. The method is only valid for a limited subset of panning angles around the perpendicular of the planned trajectory. Furthermore, uncertainties in the stereoscopic baseline lead to inconsistencies in the final depth perceived from different viewpoints. Similar to Ishiguro, Kang and Szeliski presented a method82 to reconstruct the 3-D structure of a scene using multibase stereo obtained from randomly located panoramic samples (Fig. 16). The idea was to use stereo matching from multiple viewpoints, whose locations were mapped, to estimate an omnidirectional depth map. Fleck also described a method similar to Ishiguro’s to reconstruct a 3-D model of the scene.83 These methods were conceived for robot navigation and not to produce omnistereoscopic renderings for binocular human viewing. Fig. 16Multibase stereo reconstruction of a scene based on information acquired from multiple cylindrical panoramas.82 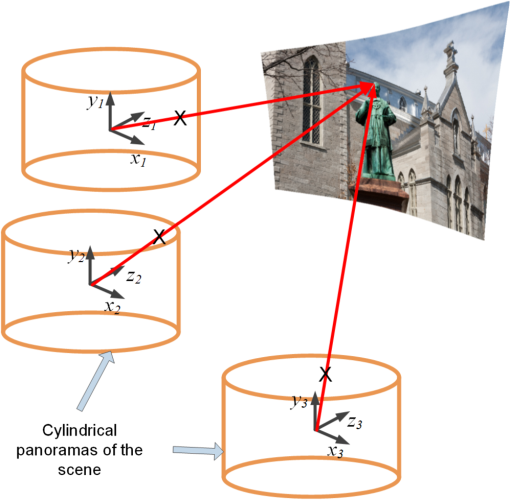 Many techniques were specifically conceived for the off-line navigation of image-based stereoscopic virtual environments. For instance, Yamaguchi et al.84 and, in a more recent follow-up, Hori et al.85 proposed a method to generate stereoscopic images based on a light-field rendering of synthetic novel views using panoramic video frames as sources. This approach enables a smooth navigation of the scene, but creates large data overhead. A key problem with this idea is that the exact position of each panoramic frame must be known a priori to find the best panoramic pair to render a binocular image for each user’s virtual location and gazing direction. In addition, it is not practically feasible to acquire the panorama frames in an accurate equally spaced grid to have control over the stereoscopic baseline. To cope with this problem, Hori et al.22 proposed capturing a panoramic video by simultaneously using two panoramic cameras mounted on a rig. Unfortunately, this approach cannot provide a full omnistereoscopic rendition of the scene, but only in directions perpendicular to the traveling path, and does not solve the data overhead problem. Vanijja and Horiguchi proposed an alternative method86 specifically tailored for a CAVE type of display. Their idea relies on a limited set of four panoramas acquired in a controlled square sampling pattern, as illustrated in Fig. 17(a), which was used to render four wide FOV panoramic images. These four partial stereoscopic views were projected on each wall of a CAVE87 to produce an omnistereoscopic immersive experience. The image patches extracted from each panorama of the cluster were arranged according to the camera panning direction in azimuth. This mapping is illustrated in Fig. 17(b). The type of display, in this case a CAVE display, imposed restrictions in terms of the number and the spatial distribution of cylindrical panoramas to use. The authors constrained the viewable stereoscopic range to certain elevation angles because the distinct cylindrical projection centers of each stereoscopic pair produced undesirable vertical disparities at low and high gazing angles in elevation. Even with these problems, this method offers advantages in terms of acquisition time and depth consistency between sampled viewpoints, making it suitable for a practical stereoscopic telepresence system. Unfortunately, this technique does not satisfy the dynamic scene acquisition constraint since individual panoramas still need to be acquired sequentially. This omnistereoscopic acquisition approach can be modeled using the central stereoscopic rig model [Fig. 3(a)], where four wide-angle (90-deg FOV in azimuth) stereoscopic snapshots of the scene are sequentially or simultaneously acquired in the directions of , 90, 180, and 270 deg to produce the image patches , for as indicated in Fig. 17. Fig. 17Vanijja and Horiguchi proposed20 using clusters of four panoramic snapshots of the scene taken in a square pattern, to extract eight wide-angle stereoscopic images to render a full omnistereoscopic image: (a) the mapping of the eight image sections from panoramas and (b) the mosaicking of these sections to create a cylindrical omnistereoscopic pair . 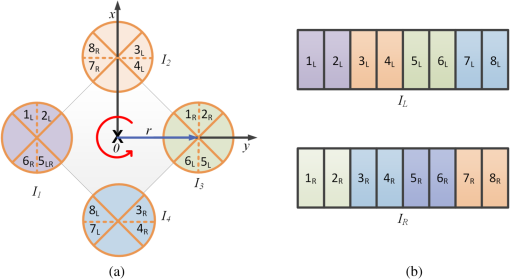 An interesting antecedent of the method of Vanijja et al. can be found in a patent application by Baker et al.14 in 2003, which was granted in 2007. This omnistereoscopic camera proposal is built around four panoramic cameras in a square pattern. The camera is shown in Fig. 18(a) illustrating four panoramic cameras in a square distribution. The arrangement simultaneously acquires four cylindrical panoramas that are used to compose four wide-angle stereoscopic views of the scene as is illustrated in Fig. 18(b) and 18(c). Although this is a multicamera system, it is relevant to include it in this section since it is a parallelization of the sequential method proposed by Vanijja et al. three years later.20 It should be mentioned that this configuration has a minimum distance to the camera where correct stereoscopic acquisition is possible; however, it has the potential to produce omnistereoscopic images of dynamic scenes. Another drawback is its fixed stereoscopic baseline, which limits its use to certain scenes. This is a good candidate for the real-time omnistereoscopic acquisition of dynamic scenes, but no attempt has been done in formalizing the stereoscopic image formation of this camera. Fig. 18The omnistereoscopic camera patented by Baker on behalf of Image Systems Inc.14 proposed a parallel acquisition of a panoramic cluster that precedes Vanijja and Horiguchi’s proposal:86 (a) using four panoramic cameras in a square pattern to simultaneously acquire four overlapping cylindrical panoramic snapshots of the scene, (b) a possible rendering strategy using sections of each cylindrical panorama to render stereoscopic close-ups, and (c) alternative with a slightly larger baseline, but where the regions for stereoscopic rendering are farther from the camera. 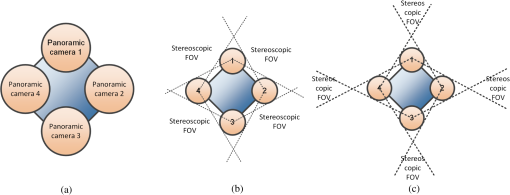 A different approach, also based on using a cluster of cylindrical panoramas of the scene in a controlled pattern, was proposed by the authors of this paper.21 Our omnistereoscopic technique was designed to reduce the acquisition time and improve the overhead efficiency. The idea improves upon the method proposed by Vanijja et al.86 by using clusters of three coplanar cylindrical panoramic snapshots of the scene. Each cluster has an equilateral triangular pattern, where each side length is directly related to the desired stereoscopic baseline. The triangular cluster is shown in Fig. 19(a), where the projection centers of each cylindrical panorama are at the vertices of the triangle. Once the panoramas are aligned,81 it is possible to map and extract stereoscopic images from pairs of panoramas within the cluster as a function of the panning direction, similar to Vanijja’s method. A similar idea based on panoramic triad was suggested by Zhu in 2001.1 An example of this mapping for a triad of cylindrical images is illustrated in Fig. 19(b), where each image section of panoramas corresponds to a particular camera panning direction in azimuth. Mosaicking these six pairs of images renders a full omnistereoscopic view of the scene in a fraction of the time needed by sequential methods based on acquiring an omnistereoscopic image column-wise. This method can be modeled by the central stereoscopic rig acquisition method [Fig. 3(a)], where six stereoscopic pairs are sampled (sequentially or simultaneously) for the panning regions indicated as , for , as indicated in Fig. 19. Fig. 19Omnistereoscopic images using a cluster of three panoramas: (a) three cylindrical panoramas in a coplanar, triangular pattern can be used to extract six image sections, and then mosaicking them using the sequence illustrated in (b) to create two novel stereoscopic views . 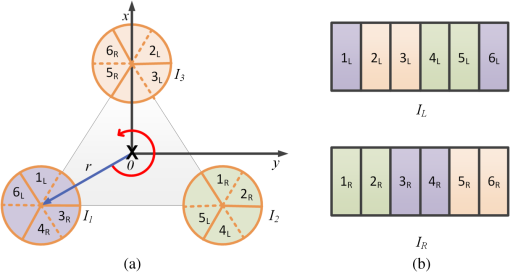 5.1.Pros and Cons of Using Panoramic SourcesAlthough the sequential methods based on panoramic sources are not suitable to acquire dynamic scenes, some of them can be adapted to multisensor configurations using wide-angle cameras. This is the case of clusters of panoramas where the distance and spatial location between projection centers are precisely known. An example of this parallelization in the acquisition is the camera proposed by Baker et al.14 using four panoramic sources and the sequential approach proposed by Vanijja et al.20 using the same square pattern. Similar parallelization can be applied to the authors’ own proposal of using triangular clusters of coplanar cylindrical panoramas. The main cons of using panoramic sources to extract wide-angle stereoscopic views of the scene are the natural self-occlusion between panoramas in parallel acquisition approach that leads to large data overhead. 6.Omnistereo Based on Multicamera ConfigurationsThe earlier antecedents of using multiple cameras to compose a wide-angle stereoscopic image date back to 1965, when Clay was granted a patent13 for a camera designed to capture wide-angle stereoscopic images. Although this camera was not conceived to produce omnistereoscopic imagery, it is one of the earliest antecedents of panoramic (in the wide-angle sense) stereoscopic photography to the best of our knowledge. The device illustrated in Fig. 20(a) is made of a multitude of cameras. The different optical axes converge in the direction of the object or ROI to photograph; each camera captures the image from a different viewpoint. Each camera, paired with its immediate neighbor, constitutes a stereoscopic pair. This can be taken as a precursor of a parallelization of the central stereoscopic rig acquisition method [Fig. 3(a)]. The drawback is that this configuration uses a multiplicity of narrow-angle lenses, which creates stereoscopic pairs that can only capture stereoscopic objects when they are located far from the camera. In other words, this camera acquires stereoscopic views of scenes where the distance from the camera is so large that human binocular perception is just marginal. Conversely, the foreground scene can be captured by individual cameras only; hence there is an important blind stereoscopic region. In its original conception, this idea used off-the-shelf film cameras, but a similar idea has been reused to capture multiple overlapping sections of the image from different viewpoints using lenticular arrays in front of each individual camera.35,46,64 Fig. 20Examples of omnistereoscopic cameras based on multiple sensors: (a) in an early patent from 1965, Clay exploited the overlapping FOVs between cameras with slightly different viewpoints to produce stereopsis.13 (b) Shimada and Tanahashi’s multiple-camera configuration designed to produce omnidirectional depth maps in real time.88,89 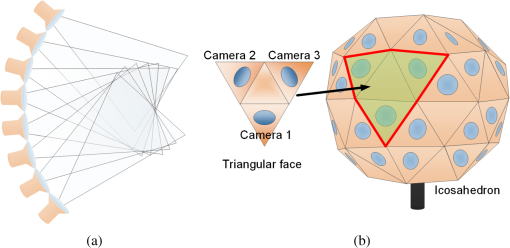 An approach for constructing a panoramic depth map using multiple cameras distributed over an icosahedric structure [Fig. 20(b)] was proposed by Shimada et al.88 and by Tanahashi et al.89,90 Each face of the icosahedron houses three cameras, determining an arrangement of 60 cameras, more specifically, 20 sets of three cameras. The authors proposed to use the stereo images from three different stereo pairs per face, e.g., grouping the three cameras in three groups of two, to create disparity maps in three spatial directions. The beauty of this idea is that only one camera per face is used to compose a spherical panorama, while each face’s estimated depth map is registered on the final spherical image. The authors of this camera configuration proposed this idea to detect movements in every direction; however, the concept of independently creating a correct panorama and a panoramic depth map can be exploited to create a synthetic omnistereoscopic image.12 The geometric distribution of cameras makes this configuration attractive to render stereoscopic panoramas in spherical format, unlike the majority of omnistereoscopic acquisition methods that focus on cylindrical topologies. The problem of acquiring spherical stereoscopic views of dynamic scenes is still open to further research. Firoozfam et al. presented a camera capable of producing omnistereoscopic images by mosaicking six stereoscopic snapshots of the scene.91 The authors of this work proposed to add omnidirectional depth estimation capabilities to their previous panoramic camera design.92 To do so, a configuration based on six stereoscopic camera rigs in a star-like hexagonal pattern was used. This camera corresponds to the off-centered stereoscopic rig acquisition model illustrated in Fig. 3(d), where stereoscopic rigs are located radially in six equality spaced angles. An illustration of their camera is shown in Fig. 21(a). A prototype of their omnistereoscopic camera, which was conceived for underwater visualization, was built circa 2002, and even calibration of the stereoscopic camera pairs were reported. Although this camera was proposed for underwater robot navigation, the possibility of real-time omnistereoscopic visualization by a remotely located human operator was foreseen. Fig. 21Multicamera examples: (a) panoramic camera configuration using multiple stereoscopic pairs in a hexagonal pattern (Baker et al.93), (b) different configurations using narrower FOV lenses and larger number of cameras, and (c) an alternative multicamera configuration proposed by the authors.12 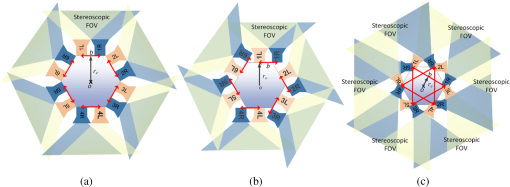 Baker et al. filed a patent application93 in 2008 on an omnistereoscopic camera using Firoozfam et al.’s concept. More specifically, their camera was also based on acquiring six partially overlapped stereoscopic images, using a star-like configuration [Fig. 21(a)]. Unfortunately, this camera configuration still lacks a theoretical framework to justify the geometric distribution of cameras. In terms of rendering, the problem of stitching images acquired from cameras with different projection points in this configuration needs to be addressed. In 2012, Baker and Constantin filed a patent application94 on a different multicamera configuration. An example of this camera is illustrated in Fig. 21(b) for 12 cameras, although the authors suggested using a larger number of cameras. As in the cases discussed above, the idea is to acquire partially overlapped stereoscopic snapshots of the scene, which can be mosaicked to render a cylindrical omnistereoscopic image. The authors suggested using 16 to 24 individual cameras with 45 to 30 deg FOV in azimuth, respectively. The distance between projection centers of adjacent cameras { and , for } can be kept smaller than in the star-like hexagonal distribution illustrated in Fig. 21(a). However, the price to pay for this increased proximity is using a larger number of cameras with narrower angle lenses to prevent self-occlusion. For example, using 24 cameras, the intercamera distance is approximately , where for a normal interocular distance, and can be smaller for hypo-stereo. The main attraction of this configuration is reducing the parallax between adjacent cameras’ projection centers while maintaining a larger baseline than the configuration in Fig. 21(a). However, using narrow-angle lenses, the minimum distance to objects in the scene is larger for stereoscopic acquisition, e.g., the distance where the scene appears in both cameras’ FOV of a stereoscopic rig. The same configuration has appeared in another recent patent application,95 but reducing the number of stereoscopic pairs by using wider angle lenses [Fig. 21(b)]. This camera can be modeled as an off-centered stereoscopic rig [Fig. 3(d)]. Our own contribution to multicamera configurations12 is illustrated in Fig. 21(c). This camera addresses the problem of creating a monoscopic panorama with respect to a common cylindrical projection center , and of acquiring accessory information to render an omnistereoscopic counterpart. The stereoscopic information follows the idea behind the approaches of Huang et al.8 and Yamada et al.,9 but uses a multisensor configuration to satisfy the real-time omnidirectional constraint of the problem. This multisensor configuration can be modeled by the lateral-radial stereoscopic rig acquisition model [Fig. 3(c)], which in this case models acquiring six stereoscopic snapshots separated in equal panning increments . The usage of wide-angle lenses helps to reduce the number of necessary stereoscopic pairs. The omnistereoscopic rendering based on the images acquired by the camera proposed in Fig. 21(c) can be done by mosaicking stereoscopic snapshots or by synthesizing a stereoscopic view in every direction based on the central panorama and the horizontal disparity and occlusion maps extracted from each stereoscopic image. The central panorama is always rendered by mosaicking images originating from cameras []. The mosaicking of the images originating from cameras [] produces a right-eye omnidirectional view of the scene, but only when the radial distance and baseline , which in this case are equivalent , are small (). This is done to prevent excessive ghosting while mosaicking the right-eye panorama. The mosaicking is a low-complexity approach suitable for real-time acquisition and rendering. The second approach involves using a larger baseline, which also implies a larger . This configuration helps to estimate horizontal depth maps and occlusion maps from each stereoscopic pair. However, the parallax between projection centers is larger and so are the stitching artifacts while mosaicking the central monoscopic view, although there are techniques to reduce these artifact.12 The second rendering alternative has advantages in terms of controlling the stereoscopic budget of the scene and the visual comfort in postprocessing that make it attractive. Tzavidas et al.57 were one of the first to attempt to parallelize the central stereoscopic rig acquisition method [Fig. 3(a)] using a multicamera approach. Their idea is based on using a large number of radially distributed cameras, as is depicted in Fig. 22(a). They proposed to use a minimum of cameras to capture snapshots of the scene. Similar to Ishiguro and Peleg’s method described in Sec. 4, Tzavidas et al.’s idea is based on extracting a pair of image columns from each image. The concept is illustrated in Fig. 13(b). These image columns are defined by the back-projection of the scene from each camera’s own projection center onto two new projection centers , for the left- and right-eye viewpoints with horizontal parallax . The idea is to mosaic the columns of to render a cylindrical left-eye panorama , and following the same procedure, mosaic the columns of to generate the right-eye panorama . Since each individual image column must be larger than one pixel, noticeable artifacts appear in the panorama after mosaicking. However, the larger the number of cameras , the narrower the image column width pixels and the smoother would be. On the same idea, Peer and Solina96 estimated that a cylindrical stereoscopic panorama of width 1680 pixels can be rendered by mosaicking image columns -pixels wide extracted from cameras in a circular radial configuration. The latter estimation is perhaps too optimistic to produce good results. The large number of cameras that may be necessary to produce an acceptable omnistereoscopic image has discouraged this approach. Fig. 22Multicamera configurations: (a) the camera configuration proposed by Tazvidas et al.57 in 2002, (b) the omnistereoscopic camera concept developed at the École Polytechnique Fédérale de Lausanne,97,98 and (c) spherical configuration proposed by Pierce et al. in a patent application.99 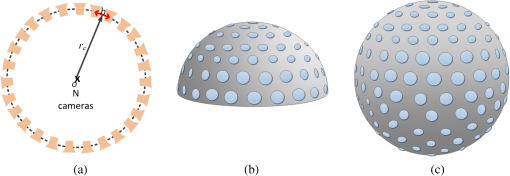 There have been different multicamera configurations based on distributing a multiplicity of cameras on 3-D surfaces as with Shimada and Tanahashi’s icosahedric camera. One of them, using a semi-spherical surface housing 104 evenly distributed cameras, has been built at the École Polytechnique Fédérale de Lausanne.97,98 The hemispherical camera, which resembles a multifaceted insect eye, is illustrated in Fig. 22(b). It was conceived to produce polycentric spherical panoramas by mosaicking a large number of snapshots. Furthermore, the developers of this camera propose to estimate the 3-D structure of the scene using stereo images extracted from pairs of cameras in selected directions. The fact that the optical axes of adjacent cameras are divergent is not an obstacle to reconstruct a 3-D depth map, although it poses a problem to compose stereoscopic images for human viewing. In a recent development,98 this camera was used to reconstruct stereoscopic panoramas in cylindrical format. However, it is necessary an analysis of the omnidirectional depth distortions after mosaicking multiple stereoscopic images captured by cameras pairs with divergent optical axes. Similar to the insect-eye camera, Pierce et al.99 proposed an omnistereoscopic camera based on a spherical surface covered with a large number of narrow-angle cameras. The idea is to compose an omnistereoscopic image by mosaicking multiple adjacent images, e.g., one camera corresponds to the left-eye view while the immediate horizontal neighbor corresponds to the right-eye view. Following this reasoning, one subset of cameras is mosaicked to form a left-eye spherical panorama while the images originating from the immediate (horizontal) neighbor are mosaicked to form the right-eye panoramic view. The fact that the adjacent cameras taken in pairs have divergent optical axes, instead of parallel or convergent optical axes, seems to be ignored by the authors. There is neither a binocular model of the image formation nor rendering examples to support the authors’ claims. In an attempt to reduce the number of cameras involved to produce omnistereoscopic imagery, Grover patented a multiple-camera system using a lenticular array,46 which is based on principles similar to Peleg’s spiral lens configuration.35 Grover’s optical approach is based on sampling interleaved image blocks corresponding to left- and right-eye views over a single 2-D planar sensor instead of capturing vertical columns corresponding to left- and right-eye views. Using high-resolution sensors and a high-density lenticular array, it would be, in theory, possible to de-interleave left- and right-eye views from each camera, mosaicking a complete omnistereoscopic image. One of the main problems with this configuration is the complexity of building and calibrating the lenticular arrays. Another major problem is the fixed stereoscopic baseline of this camera, which can lead to undesirable effects in the stereoscopic composition. Furthermore, the number of cameras necessary given a particular lenticular array and the problems of mosaicking these segmented stereoscopic views have not been determined, nor has the omnistereoscopic imagery been made available as proof of concept of this device. In a recent proposal,100 a camera composed of four fisheye lenses in a star-like configuration has been suggested to produce omnistereoscopic imagery. The designers of this camera propose to use the overlapping areas between adjacent images to extract stereoscopic views of the scene. Each image requires 180 deg FOV in azimuth or more, so each of them overlaps over at least 90 deg FOV in azimuth with the adjacent image. The authors of this conceptual camera propose to mosaic these overlapped stereo views, after correcting each lens distortion, to create a full stereoscopic spherical panorama. This is a work that is in progress at the moment of writing this paper; hence there are still many issues to be addressed. For instance, the modeling of stereoscopic views for the poles of the spherical view has not been contemplated. In general, a model for the 3-D human binocular viewing is necessary to explain this camera configuration as well as other configurations reviewed herein. Additionally, the disparity distortion due to using fisheye lenses when trying to maintain a consistent and continuous depth perception in every direction has not been addressed. Finally but not least important, a valid method to render stereoscopic panoramas by mosaicking four wide-angle images originating in different viewpoints needs to be proposed. 6.1.Pros and Cons of Multicamera ConfigurationsThe parallelization of the central stereoscopic rig acquisition method57 would be an interesting option, especially given the trend in miniaturization of high-quality cameras. The reason for being skeptical about this approach is simple: the narrower the images’ vertical stripes used to extract two parallax views of scene, the better the quality of mosaicking, but the necessary number of cameras to be able to extract narrow image columns is too large to be practical. A radial arrangement to capture partially overlapped stereoscopic images using reasonably large baselines implies a careful design of the camera geometry. Multiple-camera configurations using this strategy have been proposed recently.12,14,46,93,94 However promising, there are still unsolved issues regarding the cameras’ parallax effect in the rendering of intermediate views between samples, e.g., stitching panning directions, and maintaining the disparity continuity. Moreover, the effect of the geometric distribution of cameras on the minimum distance to objects on the scene for a correct stereoscopic viewing has not been properly studied. Another point to be considered when mosaicking wide-angle stereoscopic samples is the distortion incurred in creating a cylindrical stereoscopic panorama by mosaicking a limited number of partially overlapped stereoscopic snapshots. The conclusions of this background research in terms of the potential of each panoramic camera to acquire dynamic scenes omnistereoscopically are summarized in Table 1. Table 1Comparison between different omnistereoscopic methods.
7.ConclusionThis paper has presented a comprehensive review of methods to acquire the necessary visual information from a scene to render stereoscopic omnidirectional images, mostly in the form of cylindrical panoramas. The different proposals for omnistereoscopic acquisition have been reviewed with an emphasis on their direct or indirect potential to render stereoscopic snapshots of dynamic scenes in any panning direction. Our review rests on two separate classifications of the proposed methods. The first is a classification into four acquisition models according to the different geometric configurations used to acquire stereoscopic pairs in all directions. The second is a classification into four families based on the camera construction and/or the acquisition strategy. The paper contains four main sections reviewing proposals from the technical and patent literature belonging to these four families, identifying the acquisition model corresponding to each proposed camera configuration and discussing the relative strengths and weaknesses of each family. SVP catadioptric cameras are the most attractive for their reduced hardware, using a single image sensor, but the omnistereoscopic alternatives based on vertical coaxial configurations are not suitable to produce horizontal stereoscopic views of the scene. The omnistereoscopic catadioptric cameras are suitable to acquire panoramic depth maps, but their incapability to handle occlusions render the information acquired by these cameras incomplete, at least in the context of the problem investigated. Sequential acquisition methods were reviewed because of their potential to be adapted for a real-time omnistereoscopic sampling of dynamic scenes. Following this idea, there were interesting proposals of using multiple cameras to extract left- and right-eye views in every direction simultaneously. These methods generally underestimate the number of cameras necessary to produce artifact-free omnistereoscopic pairs. A simpler and more efficient approach is sampling the scene with a limited number of partially overlapped stereoscopic snapshots, which is the concept behind multiple-camera configurations. Before discussing the multiple-camera methods, another approach has been presented—using multiple panoramic snapshots to render omnistereoscopic images. This approach also has intrinsic problems to render omnistereoscopic views of dynamic scenes since it is based on the sequential acquisition of panoramic snapshots. The idea is to use stereoscopic wide-angle views of the scene obtained from different panoramas to create stereoscopic views in arbitrary gazing directions. When the panoramas are acquired in a known sampling pattern, the consistency in the perceived depth can be guaranteed. Since multiple wide-angle snapshots of the scene can be strategically acquired to cover all looking directions, the panoramic cluster approach can be replaced by a set of multiple stereoscopic camera pairs strategically oriented to cover the whole scene. Multiple-camera configurations are probably the best candidates in the context of the proposed problem. There are many variants of the same idea, but all of them are based on synchronously acquiring a set of partially overlapped stereoscopic snapshots of the scene. The geometric distribution between cameras varies between proposals, and there is no theoretical framework to contrast them. The lack of a formal analysis also extends to the omnistereoscopic rendering methods, which are intrinsically linked to each multiple-camera geometry. Furthermore, a model representing the binocular visual field derived from the plenoptic function model will be useful to contrast the different acquisition strategies and rendering results. AcknowledgmentsThis work was supported by the Ontario Graduate Scholarship fund and by the Natural Sciences and Engineering Research Council of Canada. ReferencesZ. Zhu,
“Omnidirectional stereo vision,”
in Proc. of the 10th International Conf. on Advanced Robotic—Workshop on Omnidirectional Vision,
1
–12
(2001). Google Scholar
C. DemonceauxP. VasseurY. Fougerolle,
“Central catadioptric image processing with geodesic metric,”
Image Vis. Comput., 29
(12), 840
–849
(2011). http://dx.doi.org/10.1016/j.imavis.2011.09.007 IVCODK 0262-8856 Google Scholar
Point Grey Research Inc., “Ladybug2,”
(2013) http://www.ptgrey.com/products/ladybug2/ ( June ). 2013). Google Scholar
R. O. Reynolds,
“Design of a stereo multispectral CCD camera for Mars Pathfinder,”
Proc. SPIE, 2542 197
–206
(1995). http://dx.doi.org/10.1117/12.218677 PSISDG 0277-786X Google Scholar
F. Hongfeiet al.,
“Immersive roaming of stereoscopic panorama,”
in Proc. Int. Conf. on Cyberworlds 2008,
377
–382
(2008). Google Scholar
H. IshiguroM. YamamotoS. Tsuji,
“Omni-directional stereo,”
IEEE Trans. Pattern Anal. Mach. Intell., 14
(2), 257
–262
(1992). http://dx.doi.org/10.1109/34.121792 ITPIDJ 0162-8828 Google Scholar
S. PelegM. Ben-Ezra,
“Stereo panorama with a single camera,”
in Proc. IEEE Conf. Computer Vision Pattern Recognition,
395
–401
(1999). Google Scholar
H.-C. HuangY.-P. Hung,
“Panoramic stereo imaging system with automatic disparity warping and seaming,”
Graphical Models Image Process., 60
(3), 196
–208
(1998). http://dx.doi.org/10.1006/gmip.1998.0467 CGMPE5 1049-9652 Google Scholar
K. Yamadaet al.,
“Generation of high-quality stereo panoramas using a three-camera panorama capturing system,”
J. Inst. Image Inf. Televis. Eng., 55
(1), 151
–158
(2001). http://dx.doi.org/10.3169/itej.55.151 1342-6907 Google Scholar
K. Yamada,
“Structure analysis of natural scenes using census transform and region competition,”
Proc. SPIE, 4310 228
–237
(2000). http://dx.doi.org/10.1117/12.411800 PSISDG 0277-786X Google Scholar
K. Yamada,
“Virtual view generation of natural panorama scenes by setting representation,”
Proc. SPIE, 4660 300
–309
(2002). http://dx.doi.org/10.1117/12.468043 PSISDG 0277-786X Google Scholar
L. E. GurrieriE. Dubois,
“Stereoscopic cameras for the real-time acquisition of panoramic 3d images and videos,”
Proc. SPIE, 8648 86481W
(2013). http://dx.doi.org/10.1117/12.2002129 PSISDG 0277-786X Google Scholar
S. Nayar,
“Catadioptric omnidirectional camera,”
in IEEE Computer Society Conf. on Computer Vision and Pattern Recognition,
482
–488
(1997). Google Scholar
S. BakerS. Nayar,
“A theory of catadioptric image formation,”
in Proc. of the 6th Int. Conf. on Computer Vision,
35
–42
(1998). Google Scholar
V. S. Nalwa,
“A true omnidirectional viewer,”
(1996). Google Scholar
V. VanijjaS. Horiguchi,
“A stereoscopic image-based approach to virtual environment navigation,”
Comput. Internet Manage., 14
(2), 68
–81
(2006). Google Scholar
L. E. GurrieriE. Dubois,
“Efficient panoramic sampling of real-world environments for image-based stereoscopic telepresence,”
Proc. SPIE, 8288 82882D
(2012). http://dx.doi.org/10.1117/12.908794 PSISDG 0277-786X Google Scholar
M. HoriM. KanbaraN. Yokoya,
“Arbitrary stereoscopic view generation using multiple omnidirectional image sequences,”
in Proc. IEEE Int. Conf. Pattern Recognition,
286
–289
(2010). Google Scholar
D. Southwellet al.,
“Panoramic stereo,”
in Proc. IEEE Int. Conf. Pattern Recognition,
378
–382
(1996). Google Scholar
J. GluckmanS. NayarK. Thoresz,
“Real-time omnidirectional and panoramic stereo,”
in Proc. of DARPA Image Understanding Workshop,
299
–303
(1998). Google Scholar
W. StürzlH. DahmenH. A. Mallot,
“The quality of catadioptric imaging application to omnidirectional stereo,”
Lec. Notes Comput. Sci., 3021 614
–627
(2004). http://dx.doi.org/10.1007/b97865 LNCSD9 0302-9743 Google Scholar
H. IgehyL. Pereira,
“Image replacement through texture synthesis,”
in Proc. of Int. Conf. on Image Processing,
186
–189
(1997). Google Scholar
T. Kawanishiet al.,
“Generation of high-resolution stereo panoramic images by omnidirectional imaging sensor using hexagonal pyramidal mirrors,”
in Proc. of the 14th Int. Conf. on Pattern Recognition,
485
–489
(1998). Google Scholar
J. Shimamuraet al.,
“Construction of an immersive mixed environment using an omnidirectional stereo image sensor,”
in Proc. IEEE Workshop Omnidirectional Vision,
62
–69
(2000). Google Scholar
L. Spacek,
“Coaxial omnidirectional stereopsis,”
in Computer Vision (ECCV),
354
–365
(2004). Google Scholar
, “Multiview generation for 3D digital signage,”
(2013) http://www.hhi.fraunhofer.de/fields-of-competence/image-processing/applications/multiview-generation-for-3d-digital-signage.html ( June ). 2013). Google Scholar
O. Scheeret al.,
“Geometrical design concept for panoramic 3D video acquisition,”
in 20th European Signal Processing Conf.,
2757
–2761
(2012). Google Scholar
, “2D&3D OmniCam: end-to-end system for the real-time acquisition of video panoramas,”
(2013) http://www.hhi.fraunhofer.de/fields-of-competence/image-processing/applications/2d-3d-omnicam.html ( June ). 2013). Google Scholar
C. Weissiget al.,
“Advances in multimedia modeling,”
Lec. Notes Comput. Sci., 7131 671
–681
(2012). http://dx.doi.org/10.1007/978-3-642-27355-1 LNCSD9 0302-9743 Google Scholar
S. PelegY. PritchM. Ben-Ezra,
“Cameras for stereo panoramic imaging,”
in Proc. IEEE Computer Vision and Pattern Recognition,
208
–214
(2000). Google Scholar
J. M. Diamond, Guns, Germs, and Steel: The Fates of Human Societies, W. W. Norton & Company, New York, NY
(1999). Google Scholar
, “Lenticular 3D billboards,”
(2013) http://www.humaneyes.com/3d-gallery-products/ ( June ). 2013). Google Scholar
Y. PritchM. Ben-EzraS. Peleg, Foundations of Image Understanding, Kluwer Academic, Dordrecht, The Netherlands
(2001). Google Scholar
P. Bourke,
“Omni-directional stereoscopic fisheye images for immersive hemispherical dome environments,”
in Computer Games & Allied Technology,
136
–143
(2009). Google Scholar
P. Bourke,
“Capturing omni-directional stereoscopic spherical projections with a single camera,”
in 16th Int. Conf. on Virtual Systems and Multimedia,
179
–183
(2010). Google Scholar
M. S. Banks,
“Achieving near-correct focus cues in a 3D display using multiple image planes,”
in SID Symposium Digest of Technical Papers,
77
–80
(2006). Google Scholar
M. FialaA. Basu,
“Panoramic stereo reconstruction using non-SVP optics,”
Comput. Vis. Image Underst., 98 363
–397
(2005). http://dx.doi.org/10.1016/j.cviu.2004.07.015 CVIUF4 1077-3142 Google Scholar
L. BagnatoP. FrossardP. Vandergheynst,
“Optical flow and depth from motion for omnidirectional images using a TV-L1 variational framework on graphs,”
in Proc. of 16th IEEE Int. Conf. on Image Processing,
1469
–1472
(2009). Google Scholar
L. ZhangC. VazquezS. Knorr,
“3D-TV content creation: automatic 2D-to-3D video conversion,”
IEEE Trans. Broadcast., 57
(2), 372
–383
(2011). http://dx.doi.org/10.1109/TBC.2011.2122930 IETBAC 0018-9316 Google Scholar
S. PelegM. Ben-EzraY. Pritch,
“Omnistereo: panoramic stereo imaging,”
IEEE Trans. Pattern Anal. Mach. Intell, 23
(3), 279
–290
(2001). http://dx.doi.org/10.1109/34.910880 ITPIDJ 0162-8828 Google Scholar
, “Roundshot panoramic film cameras by Seitz,”
(2013) http://camera-wiki.org/wiki/Seitz Google Scholar
, “Mars Pathfinder mission—Stereoscopic panorama of Mars (QuickTime VR),”
(2013) http://science.ksc.nasa.gov/mars/vrml/qtvr_stereo.html ( June ). 2013). Google Scholar
, “Mars Pathfinder mission: stereo monster panorama,”
(2013) http://mars.jpl.NASA.gov/MPF/ops/stereopan.html ( June ). 2013). Google Scholar
, “Jet Propulsion Laboratory—NASA, Mars Pathfinder,”
(2013) http://mars.jpl.NASA.gov/MPF/sitemap/anaglyph.html ( June ). 2013). Google Scholar
, “Return to Mars @ nationalgeographic.com,”
(2013) http://www.nationalgeographic.com/features/98/mars/ ( June ). 2013). Google Scholar
O. Romainet al.,
“An omnidirectional stereoscopic sensor: spherical color image acquisition,”
in Proc. Int. Conf. Image Processing,
II–209
–II–212
(2002). Google Scholar
R. A. Ainsworthet al.,
“Acquisition of stereo panoramas for display in VR environments,”
Proc. SPIE, 7864 786416
(2011). http://dx.doi.org/10.1117/12.872521 PSISDG 0277-786X Google Scholar
R. A. Ainsworth,
“Environmental imaging: photographic capture of visual environments for virtual reality systems,”
(2013) http://www.qwerty.com/Environmental_Imaging/Index.html ( June ). 2013). Google Scholar
S. ChanA. Clark,
“Periscopic stereo for virtual world creation,”
in Proc. 6th Int. Conf on Image Processing and Its Applications,
419
–422
(1997). Google Scholar
S. TzavidasA. Katsaggelos,
“Multicamera setup for generating stereo panoramic video,”
Proc. SPIE, 4661 47
–58
(2002). http://dx.doi.org/10.1117/12.460180 PSISDG 0277-786X Google Scholar
P. PeerF. Solina,
“Panoramic depth imaging: single standard camera approach,”
Int. J. Comput. Vis., 47
(1), 149
–160
(2002). http://dx.doi.org/10.1023/A:1014541807682 IJCVEQ 0920-5691 Google Scholar
P. PeerF. Solina, Real Time Panoramic Depth Imaging from Multiperspective Panoramas Using Standard Cameras, Nova Science, New York
(2009). Google Scholar
Y. PritchM. Ben-EzraS. Peleg,
“Automatic disparity control in stereo panoramas (OmniStereo),”
in Proc. IEEE Workshop on Omnidirectional Vision,
54
–61
(2000). Google Scholar
C. WangC.-Y. ChangA. A. Sawchuk,
“Object-based disparity adjusting tool for stereo panoramas,”
Proc. SPIE, 6490 64900D
(2007). http://dx.doi.org/10.1117/12.703215 PSISDG 0277-786X Google Scholar
S. Peleg,
“Omnistereo: 3D stereo panorama,”
(2013) http://www.vision.huji.ac.il/stereo/ ( June ). 2013). Google Scholar
M. Ben-Ezra,
“Omnidirectional stereo imaging,”
(2013) http://www.ben-ezra.org/omnistereo/omni.html ( June ). 2013). Google Scholar
P. Bourke,
“Capturing omni-directional stereoscopic spherical projections with a single camera,”
in 16th Int. Conf. on Virtual Systems and Multimedia,
179
–183
(2010). Google Scholar
F. HuangR. KletteK. Scheibe, Panoramic Imaging: Sensor-Line Cameras and Laser Range-Finders, Wiley, Hoboken, NJ
(2008). Google Scholar
, “Panoscan Mark III panoramic camera,”
(2013) http://www.panoscan.com/MK3/index.html ( June ). 2013). Google Scholar
S. WeiF. HuangR. Klette,
“Determination of geometric parameters for stereoscopic panorama cameras,”
Mach. Graph. Vis., 10
(3), 399
–427
(2001). Google Scholar
F. HuangS. WeiR. Klette,
“Geometrical fundamentals of polycentric panoramas,”
in Proc. 8th IEEE Int. Conf. on Computer Vision,
560
–565
(2001). Google Scholar
F. HuangR. Klette,
“Stereo panorama acquisition and automatic image disparity adjustment for stereoscopic visualization,”
Multimed. Tools Appl., 47
(1), 353
–377
(2010). http://dx.doi.org/10.1007/s11042-009-0328-2 1380-7501 Google Scholar
S.-K. WeiF. HuangR. Klette,
“The design of a stereo panorama camera for scenes of dynamic range,”
in Proc. 16th Int. Conf. on Pattern Recognition,
635
–638
(2002). Google Scholar
F. HuangZ.-H. Lin,
“Stereo panorama imaging and display for 3D VR system,”
in Congress on Image and Signal Processing,
796
–800
(2008). Google Scholar
F. HuangA. ToriiR. Klette,
“Geometries of panoramic images and 3D vision,”
Mach. Graph. Vis., 19
(4), 463
–477
(2010). Google Scholar
W. JiangJ. Lu,
“Panoramic 3D reconstruction by fusing color intensity and laser range data,”
in 2006 IEEE Int. Conf. on Robotics and Biomimetics,
947
–953
(2006). Google Scholar
C. Barnes,
“Omnistereo images from ground based LIDAR,”
in ACM SIGGRAPH 2012 Posters SIGGRAPH ‘12,
126
(2012). Google Scholar
W. JiangS. SugimotoM. Okutomi,
“Panoramic 3D reconstruction using rotating camera with planar mirrors,”
in Proc. of Omnivis ’05,
123
–130
(2005). Google Scholar
P. Bourke,
“Synthetic stereoscopic panoramic images,”
in Interactive Technologies and Sociotechnical Systems,
147
–155
(2006). Google Scholar
K. Sarachik,
“Characterising an indoor environment with a mobile robot and uncalibrated stereo,”
in IEEE Int. Conf. on Robotics and Automation,
984
–989
(1989). Google Scholar
L. E. GurrieriE. Dubois,
“Optimum alignment of panoramic images for stereoscopic navigation in image-based telepresence systems,”
in Proc. of the 11th Workshop on Omnidirectional Vision, Camera Networks and Non-Classical Cameras,
351
–358
(2011). Google Scholar
S. B. KangR. Szeliski,
“3-D scene data recovery using omnidirectional multibaseline stereo,”
Int. J. Comput. Vis., 25
(2), 167
–183
(1997). http://dx.doi.org/10.1023/A:1007971901577 IJCVEQ 0920-5691 Google Scholar
S. Flecket al.,
“Omnidirectional 3D modeling on a mobile robot using graph cuts,”
in Proc. of the IEEE Int. Conf. on Robotics and Automation,
1748
–1754
(2005). Google Scholar
K. Yamaguchiet al.,
“Real-time generation and presentation of view-dependent binocular stereo images using a sequence of omnidirectional images,”
in Proc. IEEE Int. Conf. Pattern Recognition,
589
–593
(2000). Google Scholar
M. HoriM. KanbaraN. Yokoya,
“Novel stereoscopic view generation by image-based rendering coordinated with depth information,”
in 15th Scandinavian Conf. on Image Analysis,
193
–202
(2007). Google Scholar
V. VanijjaS. Horiguchi,
“Omni-directional stereoscopic images from one omni-directional camera,”
J. VLSI Signal Process., 42
(1), 91
–101
(2006). http://dx.doi.org/10.1007/s11265-005-4168-7 JVSPED 0922-5773 Google Scholar
C. Cruz-Neiraet al.,
“The CAVE: audio visual experience automatic virtual environment,”
Commun. ACM, 35 64
–72
(1992). http://dx.doi.org/10.1145/129888.129892 CACMA2 0001-0782 Google Scholar
D. Shimadaet al.,
“Extract and display moving object in all direction by using stereo omnidirectional system (SOS),”
in Proc. the 3rd Int. Conf. on 3-D Digital Imaging and Modeling,
42
–47
(2001). Google Scholar
H. Tanahashiet al.,
“Development of a stereo omnidirectional imaging system (SOS),”
in Proc. of the 26th Conf. of the IEEE Industrial Electronics Society,
289
–294
(2000). Google Scholar
H. Tanhashiet al.,
“Acquisition of three-dimensional information in a real environment by using the stereo omni-directional system (SOS),”
in Proc. of 3-D Digital Imaging and Modeling,
365
–371
(2001). Google Scholar
P. FiroozfamS. NegahdaripourC. Barufaldi,
“A conical panoramic stereo imaging system for 3-D scene reconstruction,”
in Proc. of OCEANS 2003,
2303
–2308
(2003). Google Scholar
S. Negahdaripouret al.,
“Utilizing panoramic views for visually guided tasks in underwater robotics applications,”
in MTS/IEEE Oceans01,
2593
–2600
(2001). Google Scholar
P. PeerF. Solina,
“Towards a real time panoramic depth sensor,”
Lec. Notes Comput. Sci., 2756 107
–115
(2003). http://dx.doi.org/10.1007/b13427 LNCSD9 0302-9743 Google Scholar
H. Afshariet al.,
“Hardware implementation of an omnidirectional camera with real-time 3D imaging capability,”
in 3DTV Conf.: The True Vision—Capture, Transmission and Display of 3D Video,
1
–4
(2011). Google Scholar
W. Fenget al.,
“Panoramic stereo sphere vision,”
Proc. SPIE, 8662 866206
(2013). http://dx.doi.org/10.1117/12.2004580 PSISDG 0277-786X Google Scholar
Biography Luis E. Gurrieri received his BEng in electronic engineering from the University of Buenos Aires in 1998 and an MSc in electrical engineering from the University of Manitoba in 2006. From 1998 to 2005, he worked in IT and telecommunication companies, including Ericsson and AT&T. From 2005 to 2009, he was a research engineer at the Communications Research Center in Ottawa, Canada. He is currently working toward his PhD degree in electrical and computer engineering at the University of Ottawa, where his main research area is stereoscopic vision for image-based telepresence.  Eric Dubois is a professor at the School of Electrical Engineering and Computer Science, University of Ottawa, Canada. His research has centered on the compression and processing of still and moving images, and on multidimensional digital signal processing theory. His current research is focused on stereoscopic and multiview imaging, image sampling theory, image-based virtual environments, and color signal processing. He is a fellow of IEEE, of the Canadian Academy of Engineering, and of the Engineering Institute of Canada, and is a recipient of the 2013 George S. Glinski Award for Excellence in Research of the Faculty of Engineering. |