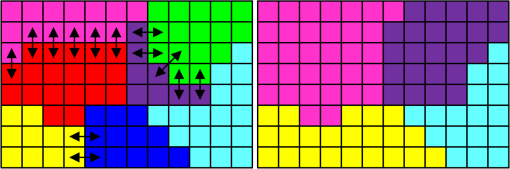
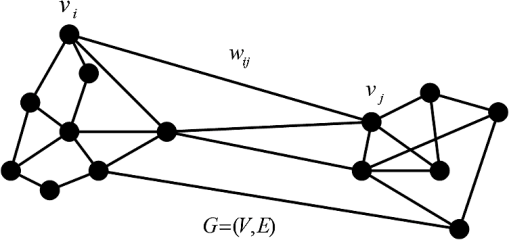
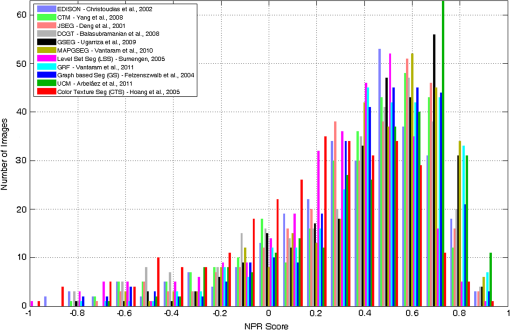
|
|
1.IntroductionColor image segmentation facilitates the separation of spatial-spectral attributes contained in images into their individual constituents; a task that is accomplished quite comfortably by our visual system and cortical mechanisms. However, mimicking this capability of human observers in an artificial environment has been found to be an extremely challenging problem. Formally, color image segmentation is defined as the process of partitioning or segregating an image into regions (also called as clusters or groups), manifesting homogeneous or nearly homogeneous attributes such as color, texture, gradient as well as spatial attributes pertaining to location. Fundamentally, a segmentation algorithm for an image is said to be “complete” when it provides a unique region or label assignment for every pixel, such that all pixels in a segmented region satisfy certain criteria while the same principles are not universally satisfied for pixels from disjoint regions. The cardinal motivation for image segmentation is twofold. It not only provides an end user with the flexibility to efficiently access and manipulate individual content, but also furnishes a compact representation of the data wherein all subsequent processing can be done at a region/segment level as opposed to the pixel level, resulting in potentially significant computational gains. To this effect, segmentation is predominantly employed as a preprocessing step to annotate, enhance, analyze, classify, categorize, and/or abstract information from images. In general, there are many applications for color image segmentation in the image processing, computer vision, and pattern recognition fields, including content-based image retrieval (CBIR), image rendering, region classification, segment-based compression, surveillance, perceptual ranking of regions, graphics, and multimedia to name a few. Furthermore, many approaches have been developed in other modalities of imaging such as remote sensing (multi/hyperspectral data) and biomedical imaging [computed tomography (CT)], positron emission tomography (PET), and magnetic resonance imaging (MRI) data for sophisticated applications such as large area search, three-dimensional (3-D) modeling, visualization, and navigation. The exponential growth of the number of applications that employ segmentation in itself provides a strong motivation for continued research and development. In the context of color imagery, segmentation is often viewed as an ill-defined problem with no perfect solution but multiple generally acceptable solutions due to its subjective nature. The subjectivity of segmentation has been extensively substantiated in experiments1 conducted at the University of California at Berkeley to develop an evaluation benchmark, where a database of manually generated segmentations of images with natural content was developed using multiple human observers. In Fig. 1(a), 10 images (arbitrarily named airplane, starfish, race cars, hills, boat, church, cheetah, dolphins, lake, and skydiver) from the aforementioned database are displayed. Additionally, several manually segmented ground truths with region boundaries superimposed (in green) on the original image are shown in Fig. 1(b) to 1(f). Analysis of the obtained ground truth results by Martin et al. divulged two imperative aspects: 1. an arbitrary image may have a unique suitable segmentation outcome while others possess multiple acceptable solutions, and 2. the variability in adequate solutions is primarily due to the differences in the level of attention (or granularity) and the degree of detail from one human observer to another, as seen in Fig. 1. Consequently, most present day algorithms for segmentation aim to provide generally acceptable outcomes rather than a “gold standard” solution. Fig. 1Berkeley segmentation benchmark:1 (a) original images, and (b) to (f) region boundaries of multiple manually generated segmentations overlaid on the images.  There are several excellent surveys of image segmentation strategies and practices. The studies done by Fu et al.2 and Pal et al.3 are amongst the earliest ones that have been widely popular. In their work, Fu et al.2 categorized segmentation approaches developed during the 1970s and early 1980s for gray scale images into three classes; namely, clustering, edge detection, and region extraction. On the other hand, Pal et al.3 reviewed more complex segmentation techniques established in the late 1980s and early 1990s that involved fuzzy/nonfuzzy mechanisms, markov random fields (MRFs) probabilistic models, color information as well as neural networks—all of which were still in their early stages of development. The surveys done by Lucchese et al.4 and Cheng et al.5 were among the first that exclusively provided an in-depth overview of algorithms targeted at segmenting color images, instituted throughout the 1990s. In this paper, we provide a comprehensive overview of the image segmentation realm with the goals to: 1. facilitate access to contemporary procedures and practices developed in the recent past (2001 to current), 2. establish current standards of segmentation outcomes from a qualitative and quantitative standpoint by displaying results acquired from state-of-the-art techniques, 3. discuss our view on the field as it stands today, and 4. outline avenues of future research. The remainder of this paper is organized as follows. Section 2 provides broad and specific categorizations of segmentation approaches based on their inherent methodology and illustrates experimental results derived from prominent color image segmentation algorithms. Furthermore, Sec. 3 provides a brief quantitative evaluation of the aforementioned algorithms. Finally, conclusions and future directives are presented in Sec. 4. 2.Classification of Segmentation MethodologiesSegmentation procedures can be broadly categorized from a high level perspective as well as specifically grouped based on their technical grounding (low level classification). The following subsections describe each of the two taxonomies in detail. 2.1.High-Level TaxonomyImage segmentation techniques can, in general, be broadly classified (see Fig. 2) based on: 1. the image type, 2. the extent of human interaction, 3. the manner in which the image is represented for processing, 4. the number and type of attributes used and, 5. the fundamental principle of operation. The first criterion segregates algorithms that have been developed for monochrome (or single band) images from the ones that handle color (or three band) images. The second criterion distinguishes methods that require human intervention (supervised processes) for segmentation from the ones that operate without any manual interference (fully automatic or unsupervised processes). The third criterion separates segmentation procedures that directly operate on the original image (single scale configuration) from the ones that operate on multiple representations of the image (multiscale configuration), each manifesting different amount of information. The fourth criterion differentiates algorithms based on the type of image information (e.g., gray/color intensity, gradient/edge, or textural features) utilized to perform the segmentation. It is imperative to note that most methods use the aforementioned image attributes individually (single attribute methods) or in specific combinations (multiple attribute methods) to categorize them. Finally, the last criterion based on the underlying principle of operation discriminates segmentation mechanisms as being either spatially blind or spatially guided. Spatially blind approaches as the name suggests are techniques that are “blind” to spatial information, or, in other words, do not take into account the spatial arrangement of pixels in an image. Instead these methods rely heavily on grouping image information in a suitable attribute/feature space. On the other hand, spatially guided approaches tend to exploit the spatial arrangement of pixels in an image during the segmentation process. 2.2.Low-Level TaxonomyAs mentioned previously, most segmentation modus operandi can be viewed as being either spatially blind or spatially guided. It is this distinction that forms the basis of our low-level taxonomy where we specifically group segmentation procedures based on their technical components, as depicted in Fig. 3. 2.2.1.Spatially blind approachesSpatially blind approaches perform segmentation in certain attribute/feature spaces, predominantly related to intensity (gray or color). Popular segmentation techniques that fall within the notion of being spatially blind involve clustering and histogram thresholding. ClusteringIn its simplest form, clustering is a spatially blind technique wherein the image data is viewed as a point cloud on a one-dimensional (1-D) gray scale axis or in a 3-D color space (see Fig. 4) depending on the image type. Several different color spaces—such as RGB, Commission International de l’Eclairage (CIE) and , , HSI etc., to name a few—with different properties have been extensively utilized for segmentation.6 The essence of a typical clustering protocol is to analyze this gray/color intensity point cloud and partition it using predefined metrics/objective functions to identify meaningful pixel groupings also known as classes or clusters. Furthermore, the clustering process is done such that, when complete, the pixel data within a specific class possess, in general, a high degree of similarity while the data between classes has low affinity. The biggest advantage of clustering approaches over others is inherent in their simplicity and ease of implementation. However, since the point clouds generated are image dependent, selecting/initializing the number of clusters so as to obtain semantic partitioning with respect to the image being processed is a challenging task, especially in the case of color imagery. Furthermore, as the dimensionality of the feature space is increased exponentially, acquiring definitive clusters becomes an arduous task. Although many clustering approaches have been developed for various applications, partitioning a feature space using a specific set of fixed points is the most widely adopted approach. Voronoi tessellation (VT) is a procedure in which a feature space is decomposed into various clusters (called Voronoi cells/regions) using a fixed set of points called sites, such that each observation in the feature space is assigned to the closest site predicated on a certain distance metric. More specifically, if is a feature space constrained with a distance function , and is a set of sites in the space, then a Voronoi cell formed using the site is the set of all points that satisfy: where represents the distance from to . Arbeláez et al.7 proposed a VT-based image segmentation technique utilizing color and lightness information derived from the image. The segmentation objective was achieved in a two-step process comprised of: 1. presegmentation and 2. hierarchical representation. The presegmentation step employed a VT process wherein the extreme components of the lightness () channel were used as sites to form an extrema mosaic of Voronoi regions. The second step involved the development of a stratified hierarchy of partitions derived from the extrema mosaic using a pseudo-distance metric called ultrametric, specifically defined for color images. Subsequently, a single real-valued soft boundary image called the ultra-metric contour map (UCM) was constructed to arrive at the final segmentation.Centroidal voronoi tessellation (CVT) is a special category of VT wherein the sites producing Voronoi cells are chosen equivalent to their center of mass. Wang et al.8 generalized the basic CVT by integrating an edge-related energy function with a classic clustering energy metric to propose an edge-weighted centroidal voronoi tessellation (EWCVT) for effective segmentation of color images. CVTs form the core of many prominent clustering algorithms such as -means. The -means algorithm partitions a set of -pixels into clusters by minimizing an objective function. From a color segmentation perspective, the aforementioned algorithm analyzes the image data in a 3-D space to eventually identify -sites (known as cluster centers or means) such that the mean squared distance from each data point to its nearest center is minimized. To this effect, in an arbitrary iteration (called as a Voronoi iteration or Lloyd’s algorithm), the entire color space is separated into partitions by assigning each observation to the cluster with the closest center (note initialization in the first iteration may be randomly done). Following this, a new estimate of the cluster center is computed based on the current cluster assignment information and is utilized as an input to the next iteration of the algorithm. The algorithmic steps described above are repeated until convergence is achieved. McQueen9 was the first to employ the -means algorithm to handle multivariate data. Among recent advances, Kanungo et al.10 proposed an efficient version of the algorithm called the “filtering algorithm,” by utilizing a k-dimensional (kd) tree representation of the image data. For each node of this tree, a set of candidate centers were determined and strategically filtered as they were propagated to the node’s children. The biggest advantage of this approach was that, since the kd-tree representation was formed from the original data rather than from the computed centers, it did not mandate an update in its structure for all iterations, in contrast to the conventional -means architecture. Chen et al.11 employed a generalization of the classical -means algorithm better known as the adaptive clustering algorithm (ACA), with spatially adaptive features pertaining to color and texture, to yield perceptually tuned segmentations. Consequently, the ACA method is an exception to the norm of spatially blind clustering. In his work, Mignotte12 proposed a novel color image segmentation procedure based on the fusion of multiple -means clustering results by minimizing the Euclidean distance function, obtained from an image described in six different color spaces namely RGB, HSV, YIQ, XYZ, LAB, and LUV. Once the label fields from each of these color spaces are obtained, a local histogram of the class labels across the aforementioned label fields is computed for each pixel, and the set of all histograms are employed as input feature vectors to a fusion mechanism that culminates in the final segmentation output. The fusion scheme is comprised of the -means algorithm using the Bhattacharya similarity coefficient, which is a histogram-based similarity metric. The algorithm in Mignotte12 was further enhanced in Mignotte13 by using a spatially constrained -means labeling process in place of the fusion mechanism to arrive at the optimal result. While the prior algorithm developed by Mignotte was aimed at exploring the possibility of integrating multiple segmentation maps from simple data partitioning models to obtain an accurate result, the later algorithm was novel in the sense that within the -means framework implicit spatial associations in an image were taken into account (similar to the work in Ref. 14) to uncover the best solution, and consequently the process was not completely spatially blind. Mean shift clustering15 is another routine that has had pervasive use for gray/color image segmentation within the last decade. This generic nonparametric technique facilitates the analysis of multidimensional feature spaces with arbitrarily shaped clusters, based on the “mean shift” concept, originally proposed by Fununaga et al.16 The mean shift procedure is a kernel density estimation (or Parzen window-based technique) that scrutinizes a feature space as an empirical probability density function (pdf) and considers the set of pixel values from an arbitrary image as discrete samples of that function. The procedure exploits the fact that clusters/dense regions in a feature space typically manifest themselves as modes of the aforementioned pdf. In what follows, if is a finite point cloud in an -dimensional Euclidean space, and is a symmetric Kernel function of specific characteristics, then the sample mean at a pixel computed utilizing a weighted combination of its nearby points determined by is given as:17 To this effect, at every pixel location , a mean shift vector is obtained with centered at , such that the vector points towards the direction of the maximum increase in density. Subsequently, the operation is performed that shifts the value of toward the mean followed by the re-estimation of . This process is repeated until convergence of is achieved. At the end of the mean shift process, the closest peak in the pdf is identified for each pixel. Since the mean shift algorithm uses spatial knowledge in its framework, it also represents an exception to conventional spatially blind clustering. Mean shift clustering guided by edge information was first seen in the work by Christoudias et al.,18 who proposed the edge detection and image segmentation (EDISON) system, aimed at improving the sensitivity of extracting homogeneous regions while maintaining or ideally minimizing over-segmentation of an image. Figure 5 illustrates a few results of the EDISON system using default parameters (spatial band , color band width , and minimum region size ). Hong et al.19 proposed an improved version of the mean shift segmentation algorithm by incorporating: 1. an enhanced technique for mode detection, 2. an optimized process for the global analysis of the locally identified modes, and 3. the elimination of textured areas in order to achieve stable results in various background conditions. Ozden et al.20 pioneered an effective technique that combined low-level color and spatial and texture features in the mean shift framework for color image segmentation. Neural networks-based data clustering is a category that has originated exclusively from the field of artificial intelligence. Within this domain, methods involving self-organizing maps (SOMs) have received the most attention in the last decade. A self-organizing map or a self-organizing feature map (SOFM)—alternately known as a Kohonen map—is a specific kind of artificial neural network (ANN) that was first introduced by Kohonen21 as a tool for providing intelligent representations of high/multi-dimensional feature spaces in significantly lower (one or two) dimensions. A SOM (shown in Fig. 6) comprises of an input layer of nodes/neurons organized in a vector whose size is equivalent to the dimensions of the input feature space. Each node is connected in parallel to a two-dimensional (2-D) output layer of neurons in a rectangular or hexagonal arrangement as well as their corresponding neighboring neurons utilizing an appropriate weighting scheme that signifies the strength of various connections. A SOM operates in a “training” phase that gradually constructs a feature map using a subset of samples from the input feature space, followed by a mapping routine in which an arbitrary new input sample is automatically classified. At the culmination of the two modes of operation, a low-dimensional map that reflects the topological relationships of samples in the feature space predicated on their similarity is subsequently generated. In other words, samples that have similar characteristics in the input feature space form distinct clusters in this map. Huang et al.22 developed a color image segmentation methodology that employed a two-stage SOM-based ANN. The algorithm is initiated by an RGB to HVC (hue-value-chroma) color conversion of the input image, which is employed by an SOM to identify a large initial set of color classes. The resultant set of classes are further refined by first computing the normalized Euclidean distance among them, and the obtained between-class distances are furnished as inputs to a second SOM that identifies the final batch of segmented clusters. In a similar scheme, Ong et al.23 constructed a color image segmentation technique based on a hierarchical two-stage SOM in which the first stage identifies dominant colors in the input image presented in the color space, while the second stage integrates a variable-sized 1-D feature map and cluster merging/discarding operations to acquire the eventual segmentation result. Li et al.24 demonstrated an effective color image segmentation approach using a SOM and the fuzzy-C-means (FCM) clustering procedure. The algorithm is initiated by finding well-suited image-dependent features derived from five different color spaces using a SOM. Subsequently, the obtained features were employed in a FCM protocol to attain the output segmentation. Dong et al.25 instituted two alternate ANN-based strategies for color image segmentation. The first strategy was unsupervised. It involved distinguishing a set of color prototypes using SOM-based learning from the input image represented in the color space. These color prototypes were passed on to a simulated annealing-driven clustering routine to yield well-defined clusters. The second method, built off the aforementioned algorithm, was coupled with hierarchical pixel learning (that generated different sizes of color prototypes in the scene) and classification protocols to provide more accurate segmentation outcomes in a supervised fashion. Partitioning of color imagery using SOM and adaptive resonance theory (ART) was first seen in the work of Yeo et al.,26 who proposed two compound ANN architectures called SOMART and SmART (SOM unified with a variation of ART) that yielded improved segmentations in comparison to traditional SOM-based techniques. On the other hand, Araújo et al.27 designed a fast and robust self-adaptive topology ANN model called local adaptive receptive field SOM (LARFSOM) that deduced compact clusters and inferred their appropriate number based on color distributions learned rapidly from the network’s training phase using a small percentage of pixels from the input image. The algorithm was tested on color images with varying segmentation complexities and was found to outperform several prior SOM-based techniques. Frisch28 introduced a novel approach robust to illumination variations that employed SOMs for the construction of fuzzy measures applicable to color image segmentation. This work was a unique attempt wherein efficient fuzzy measures, to accomplish the segmentation task, were derived using SOM-based processing. Ilea et al.29 devised a fully automatic image segmentation algorithm called CTex using color and texture descriptors. The CTex segmentation architecture first extracts dominant colors from the input image presented in the RGB and YIQ color spaces using an SOM classifier. In doing so, the appropriate number of clusters () in the scene are also identified. Subsequently, a conventional -means clustering algorithm is employed in a six-dimensional (6-D) multispace spanned by both the above stated color spaces to obtain a segmentation result purely based on color information. This is followed by the computation of textural features using a Gabor filter bank, which, along with the previously acquired segments, are provided as input to a novel adaptive spatial -means (ASKM) clustering algorithm that delineates coherent regions of color and texture in the input image. The clustering techniques discussed so far are typically categorized as hard clustering approaches since every observation in the feature space has a unique and mandatory cluster assignment yielding clusters with sharp boundaries. In contrast, significant work has been done for the advancement of fuzzy clustering methods that facilitate observations to bear a certain degree of belongingness or membership to more than one cluster, resulting in overlapping clusters and/or clusters with “soft” boundaries. The Fuzzy-C-Means (FCM) algorithm, originally developed by Dunn30 is the most widely utilized fuzzy clustering methodology and is similar to the -means technique, partitions a set of -pixels () into fuzzy clusters () by minimizing an objective function. The objective function utilized by the FCM algorithm is represented as: where From Eqs. (3) and (4) it can be inferred that the FCM objective function differs from -means by incorporating membership values for various observations in the feature space as well as a “fuzzifier” term that directs the extent of cluster fuzziness.In their work, Yang et al.31 proposed two eigen-based fuzzy clustering routines namely, separate eigenspace FCM (SEFCM) and couple eigen-based FCM (CEFCM), for segmentation of objects with desired attributes in color imagery. Given an arbitrary image with a predefined set of pixels, the color space in which the image is expressed is initially divided into two eigenspaces called principal and residual eigenspaces using the Principal Component Transformation. Following this, the SEFCM design obtains a segmentation output by integrating the results of independently applying the FCM algorithm to the aforementioned eigenspaces. The integration process involves a logical selection of common pixels from the two clustering results. On the other hand, the CEFCM arrangement obtains an output segmentation result by jointly considering the principal and residual eigenspaces. Both routines were found to outperform the traditional FCM clustering approach from a color object segmentation perspective. Liew et al.32 instituted an adaptive fuzzy clustering scheme by imposing local spatial continuity using contextual information. The method was targeted for exploiting inter-pixel correlation existent in most conventional imagery in a fuzzy framework. Chen et al.14 proposed a computationally efficient version of the FCM algorithm using a two-phase scheme involving data reduction followed by clustering. This computationally more efficient approach was found to produce results of similar quality to the conventional FCM. More recently, Hung et al.33 developed a weighted FCM (WFCM) clustering technique wherein the weights for various features were computed using a bootstrap method. Incorporating the bootstrap approach was found to provide satisfactory weights to individual features from a statistical variation viewpoint and enhance the performance of the WFCM procedure. Tziakos et al.34 proposed an approach using the Laplacian Eigen (LE) map algorithm, a manifold learning technique, to boost the performance of FCM clustering. The methodology is commenced by extracting local image characteristics from overlapping regions in a high-dimensional feature space, from which a low-dimensional manifold was learned using spectral graph theory. Following this, the LE-based dimensionality reduction technique was used to compute a low dimensional map that captured local image characteristic variations, eventually used to enhance the performance of FCM clustering. Krinidis et al.35 and Wang et al.36 developed alternate yet efficient versions of the FCM scheme that employed both local intensity and spatial information. Yu et al.37 founded an ant colony-fuzzy C-means hybrid algorithm (AFHA) for color image segmentation that adaptively clustered image elements utilizing intelligent cluster center initializations as well as subsampling for computational efficiency. The results of the AFHA structure were found to have smaller distortions and more stable cluster centroids over the conventional FCM. Besides the practices discussed so far in this section, several unique clustering-based methods for image segmentation have also been proposed. Veenman et al.38 developed an efficient and optimized model for clustering using a cellular co-evolutionary algorithm (CCA) that does not require any prior knowledge of the number of clusters. On the other hand, Allili et al.39 instituted a clustering model that combined a generalized Gaussian mixture model with a pertinent feature selection to alleviate problems of under/over segmentation. Jeon et al.40 introduced a sparse clustering method for color image data using the principle of positive tensor factorization (PTF). Aghbari et al.41 proposed a hill-manipulation process where the protocol of segmenting an arbitrary color image was treated in an equivalent fashion to that of finding hills in its corresponding 3-D intensity histogram. Ma et al.42 introduced the notion of clustering using lossy data coding and compression and demonstrated their work on natural scene color images. The algorithm in Ma et al.42 was employed by Yang et al.,43 who proposed a compression-based texture merging (CTM) routine that treated segmentation as a task of clustering textural features modeled as a mixture of Gaussian distributions, wherein the clustering methodology was acquired from a lossy data compression protocol. Sample segmentation outcomes of the CTM algorithm using default parameters (coding data length parameter ) are exhibited in Fig. 7. Huang et al.44 advocated the concept of pure “clustering-then-labeling” for efficient segmentation of color images. Histogram thresholdingHistogram thresholding [see Ref. 45 for a comprehensive survey] is a spatially blind technique primarily based on the principle that segments of an image can be identified by delineating peaks, valleys, and/or shapes in its corresponding intensity histogram. Similar to clustering, histogram thresholding protocols require minimal effort to realize in comparison with most other segmentation algorithms and function without the need for any a priori information about the image being partitioned. Owed to its simplicity, intensity histogram thresholding initially gained popularity for segmenting gray-scale images. However, during its course of development, it was found that thresholding intensity histograms did not work well for low-contrast images without obvious peaks and yielded ambiguous partitions in the presence of spurious peaks manifested by noise. Additionally, for color images, it was determined that thresholding in a multidimensional space is a difficult task. Figure 8 illustrates color histograms of the starfish and boat images in the RGB space, generated using an open-source ImageJ plugin called Color Inspector 3D.46 Each color bin in the 3-D histogram is represented as a sphere whose volume is proportional to the frequency of occurrence of that color. From the histograms, it can be observed that finding multiple thresholds to efficiently partition them presents a challenging problem. Kurugollu et al.47 proposed an algorithm for color image segmentation that involved two major steps, namely multithresholding and fusion. The method is initiated by forming 2-D histograms using pair-wise band combinations (RG, GB, and BR), each of which were subjected to a peak finding protocol. Following this, based on the delineated peaks, a multithresholding scheme was used to form a segmentation result unique to each pair of channels. These three segmentation results were fused using a label concordance algorithm and refined using a spatial chromatic majority filter to derive the final segmentation result. In a similar framework, Cheng et al.,48 designed a color image segmentation scheme, based on the idea of thresholding a homogram, which simultaneously captured the occurrence of gray levels along with adjoining homogeneity values among pixels. The segmentation routine was initiated by forming a homogram individually for each color channel, the peaks of which were used to guide a subsequent thresholding scheme to acquire an initial oversegmented set of clusters. Finally, the three sets of clustering results from the red, green, and blue planes, respectively, were united together to achieve the final segmentation. Mushrif et al.49 exploited the concept of Histon thresholding based on rough set theory to devise an efficient algorithm for color image segmentation. A Histon is defined as a set of pixels that are all potentially part of a particular segment. Their three-step architecture involved computing a Histon, followed by thresholding and culminating in a region merging process (discussed in Sec. 2.2.2.1). Additionally, they further enhanced the aforementioned methodology though the work in Mushrif et al.50 using an Atanassov’s intuitionistic fuzzy set (A-IFS) Histon representation of the input image. In their work, Manay et al.51 proposed an adaptive thresholding structure for fast segmentation using an anisotropic diffusion model based on the principle that, for an arbitrary local area, an optimal threshold can be derived close to image edges using a smooth version of it. 2.2.2.Spatially guided approachesIn contrast to spatially blind methods, spatially guided approaches, as the name suggests, are guided by spatial relationships of pixels for segmentation. Their primary objective is to form pixel groupings that are compact or homogeneous from a spatial standpoint, irrespective of their relationships in specific feature spaces. However, despite the development of many spatially guided techniques, the use of region and edge information explicitly or in an integrated framework remain widely-accepted alternatives for the formation of spatially compact regions. Segmentation techniques that distinctly use region information typically employ protocols involving growing, splitting, and merging individually or in suitable combinations. For the formation of an arbitrary region, growing is a process that starts from a single pixel or small predefined labeled set of pixels called a seed and is based on a certain homogeneity criterion iteratively accumulates pixels around it, as depicted in Fig. 9. The growth of a region stops when pixels satisfying the homogeneity criterion are no longer found. Most growing approaches help create spatially connected and compact regions relative to other routines in literature. Additionally, the established regions possess specific user-defined properties with high tolerance to noise. However, sequential design (pixel-by-pixel agglomeration) of growing procedures often results in intensive computational schemes with significant memory requirements. In addition, the presence of varying shades of colors produce, in general, oversegmented outputs. Furthermore, the quality of the segmentation is heavily dependent on the order in which the seeds are processed. In comparison with the region growing, region splitting is a technique that is initiated with an inhomogeneous segmentation of an image, which is repetitively split until segments satisfying a particular homogeneity criterion are obtained. Splitting can be achieved via diverse methods such as quadrature tree decomposition, watersheds, or implicitly via region growing when multiple seeds are placed in homogeneous areas that fall under different categories of our low-level taxonomy. Consequently, we do not explicitly group them in our discussion. The aforementioned growing and splitting procedures generally yield good results for simple images with well-defined homogeneous regions. However, utilizing them purely based on color homogeneity may, in general, pose difficulties due to varying shades of color, nonuniformity of color spaces, illumination, and texture disparities. Region merging is a process in which subregions—potentially part of a larger identifiable region—are fused together to yield a reduced set of segments that are spatially meaningful with respect to the input image content (see Fig. 10 for a simplified illustration). In general, for reasonably complex images, growing/splitting methods often result in an oversegmented region map. As a result, they are often integrated with some type of a region-merging scheme to improve the final outcome. Region-growing approachesFan et al.52 proposed an automatic image segmentation algorithm that begins with an edge detection scheme, wherein the centroids between the detected edges are chosen as the set of candidate seed points. Subsequently, a growth procedure is utilized to spatially integrate pixels, in a recursive fashion, to an appropriately chosen seed from the entire set until the final segmentation is achieved. Wan et al.53 were the first to introduce a theoretical criteria for a specific category of region growing algorithms called symmetric region growing, which are insensitive to the selection of the initial seed points. Fondón et al.54 introduced a multistep region growing procedure for color image segmentation, in which the extent of growth can be controlled using a tolerance parameter dependent on the variance of the actual grown region. Although the method was successful in accurately delineating spatial extent of regions, it necessitated manual selection of seed points and could only handle one region at a time. Qin et al.55 advocated the use of semantic information for effective region growing, and proposed an MRF-based multivariate image segmentation algorithm. Region-merging approachesSimilar to growing, a significant number of approaches have been proposed that explicitly use a merging protocol for region-based segmentation. Devaux et al.56 built a unique segmentation architecture that employed the Karhunen-Loeve transform (KLT) in combination with color and textural attributes for region-based segmentation of color aerial images. The algorithm separately exploited color and texture information to come up with two initial segmentation maps that are subsequently fused together in a merging protocol. Chen et al.57 developed a segmentation technique based on color contrast. The technique began by converting the color input image from RGB to CIE and then utilized the later computed values to estimate contrast information with four directional operators. The estimated contrast map was thresholded to identify an initial set of regions, which were appropriately merged using a connection and verification process. Nock et al.58 explored a statistical region merging structure of segmenting image data, based on the notion that perceptual grouping with region merging can be effectively used to encapsulate the big picture of a scene, using primary local glimpses of it. Nock et al.59 further enhanced the work in 2005 their work by treating statistical region merging as a nonparametric mixture model estimation problem. In his work, Kim60 devised an approach for segmenting low-depth-of-field images using morphological filters and region merging. The procedure involved an initial conversion of a low-depth-of-field image to an alternate feature space representing higher order statistics (HOS). The resultant HOS map was simplified using morphological reconstruction followed by region merging to produce the output segmentation result. Kuan et al.61 presented a novel region merging strategy for segmenting salient regions in color images. The technique generated an initial set of regions by extracting dominant colors in the input image, using a nonparametric density estimation methodology. Subsequently, a merging protocol based on “importance index” and “merging likelihood” criterions was used to refine the initial set. With a similar global objective to the work in Kuan et al.,61 Liu et al.62 proposed an unsupervised segmentation algorithm aimed at salient object extraction. The method was based on region merging in a binary partition tree (BPT) framework. It utilized a novel dissimilarity measure that considered color difference, area factor, and adjacency degree criterions. A robust termination criterion for conventional region merging algorithms based on a novel distinctness predicate of adjacent regions was proposed in Tan et al.63 The effectiveness of the aforementioned criterion was demonstrated using two new merging criteria based on local and global image characteristics. Region merging techniques using statistical measures from the field of information theory was first seen in the work of Calderero et al.64 The proposed merging protocols were unique in the fact that they did not make any assumptions of color or texture homogeneity of regions, but were characterized by nonparametric region models. Hybrid growing-merging approachesIntegration of growing and merging is another popular region-based methodology in the segmentation realm. Deng et al.65 proposed the prominently known J-SEGmentation (JSEG) algorithm that integrated color quantization and spatial segmentation for extraction of color-texture regions in images and video (see Fig. 11). The JSEG method commences in a color quantization step utilized to obtain a “color class map,” which is subsequently employed to compute a J-image based on certain spatial constraints. These spatial constraints were designed such that the resultant J-image corresponded to measurements of local homogeneities that acquired high values at region boundaries and low values for homogeneous color-texture regions. Subsequently, the J-image is utilized as a reference to identify suitable seed points to initiate a region growing process, wherein the obtained regions are eventually refined in a merging process using a color similarity criterion. Although the JSEG method was efficient in deriving spatially compact regions, it suffered from the fact that the use of color quantization caused over segmentation in regions of varying shades due to illumination or texture disparities, as viewed in some of the results of Fig. 11 (see cheetah, skydiver, and lake images). The segmentation outcomes displayed in Fig. 11 were obtained using default parametric settings, where the parameters named color quantization threshold (qthresh) and number of scales (Iscale) are, by default, automatically computed, while the region merge threshold parameter (mthresh) was set equivalent to 0.4. The aforementioned drawback of the JSEG technique to a certain extent was addressed by Wang et al.,66 who advocated the use of mean shift clustering instead of color quantization for improved results. In their work, Wang et al.67 uncovered another drawback of the JSEG procedure by demonstrating that ignoring color discontinuity in the computation of the J-measure caused over-segmented results. To overcome this deficiency, they proposed a novel hybrid measure for homogeneity. Amidst other hybrid approaches, Cheng68 postulated a segmentation procedure for color image data in a growing-merging framework integrated with 3-D clustering and relaxation labeling. Shih et al.69 developed a segmentation algorithm based on seeded region growing and merging, incorporating strategies to avoid pixel order dependencies. He et al.70 employed the concept of gradient vector flow (GVF) in a seeded region growing and region adjacency graph (RAG)-based merging architecture. Dynamic color gradient thresholding (DCGT) integrated with a growing-merging scheme was first seen in the work by Balasubramanian et al.71 The DCGT technique was used to guide a region growth procedure for the formation of an initial set of regions, which were further refined in a merging protocol. Both steps were performed purely based on color information. To this effect, the DCGT algorithm faced problems of oversegmentation due to the lack of a texture descriptor and was computationally expensive. Figure 12 portrays the segmentation outcomes achieved from the DCGT algorithm using default parametric values described in Balasubramanian et al.71 More recently, Ugarriza et al.72 proposed a novel Gradient SEGmentation (GSEG) algorithm, which simultaneously laid emphasis on the homogeneous and heterogeneous characteristics of image data using color-texture-gradient attributes and did not exclusively depend on the initial assignment of clusters to arrive at the final segmentation (see Fig. 13). Region formation in the GSEG method was done using a unique growing approach based on the principle of dynamic gradient thresholding that iteratively thresholded gradient information derived from the image, commencing at pixel clusters with small gradient magnitudes (gradually varying intensity) and culminating at pixels groupings possessing large gradient magnitudes (abrupt intensity variations) with no dependency in the order in which they were processed. Another aspect of their growth approach different from conventional approaches was the dynamic seed addition component that accommodated simultaneous growth of several adjacent and/or nonadjacent image regions. The resulting regions were optimized using an efficient region merging approach based on statistical analysis of a multivariate space involving the aforementioned attributes. The work in Ugarriza et al.72 was enhanced by Vantaram et al.73 who proposed a multiresolution extension of the GSEG methodology called MAPGSEG and demonstrated that the segmentation results of low-resolution images can be utilized to efficiently partition their corresponding high-resolution counterparts. Overall, the MAPGSEG framework was shown to achieve, in general, comparable segmentation results to the GSEG algorithm (as seen in Figs. 13 and 14) at half its computational expense. The parametric settings utilized to achieve the results depicted in Figs. 13 and 14 have been detailed in Ugarriza et al.72 and Vantaram et al.73 Krinidis et al.74 instituted an approach for color texture image segmentation in a growing-merging schema based on a 3-D physics-based deformable surface model derived from intensity and spatial information of images. Color image segmentation using the dual tree complex wavelet transform (DT-CWT) integrated with a growing-merging strategy was seen in Celik et al.75 The partitioning process was initiated by the DT-CWT computation that enabled multiscale edge detection, wherein the acquired edges were subjected to binary morphological operations to locate suitable seed points. These seed points were employed in a region-growing approach to delineate an initial set of regions, which were fine-tuned in a subsequent merging process. Recently, Panagiotakis et al.76 devised a scheme for natural image segmentation in a growing-merging structure based on tree equipartion and Bayesian flooding processes for feature extraction. Additionally, several hybrid region-based approaches77–84 have also been proposed. In contrast to the segmentation approaches discussed in the last three subsections, energy-based segmentation techniques aim to minimize explicit cost functions. They can, in general, be classified into ones that explicitly utilize edge/contour-based energy (e.g., active contours) or ones that employ region-based energy to delineate different regions (e.g., Mumford-Shah formulation and Bayesian techniques like MRFs. Active contoursWithin the notion of using edge/contour-based energy, curve evolution methods involving active contours better known as “evolving fronts” have gained tremendous popularity over the last decade. From a high-level viewpoint, active contours can be categorized based on their implementation as being either parametric active contours (PACs) or geometric active contours (GACs). PACs are generally represented in a Lagrangian formulation where the evolving curves are called “snakes,” a concept first introduced by Kass et al.85 A snake is defined as a curve or a deformable spline that constantly moves/evolves based on a specific energy model until it attains a shape that best fits an object (or multiple objects) of interest in the scene. This energy functional typically comprises of internal () and external () energy terms as shown in Eqs. (5) and (6), whose combined effect drives a snake towards the boundary of an object resulting in the overall energy being minimized, given as: In the aforementioned equations, symbolizes the coordinates of a snake in the image domain, while is proportional to its arc length. Furthermore, is contour-dependent. It is utilized to control its tension and rigidity via parameters , , respectively, and is minimized when a snake possesses a shape that is in close proximity to the object of interest. On the other hand, is explicitly calculated in the image domain and is minimized when the physical location of a snake is along the boundaries of the object of interest. Among PACs, there exists a class of snakes called region-based active contours given that they are designed to attract to boundaries that distinguish homogeneous regions. Since its inception, it has been uncovered that the traditional snake model suffers from two major drawbacks that derail it from converging on the desired object of interest. The first occurs when the contour initialization is far from the true object boundary, and the second is when the object of interest has cavities that are concave in nature. To overcome the first shortcoming, multiresolution methods and pressure forces, as well as several enhanced models such as balloon/distance snake models, have been proposed. On the other hand, methods involving GVF and directional snake models have been offered to account for the second deficiency. PACs have several merits over classical segmentation techniques such as: 1. they are self-accommodative in their pursuit for a global energy minimum, 2. they can be easily molded via the term as needed, 3. they can be designed to be image scale dependent, and finally 4. they are not biased toward any particular object/region shape and consequently are effective for segmenting/tracking objects in spatio-temporal dimensions. Major potential demerits of PACs include: 1. brazing localized energy minima, 2. ignoring minor image features for global energy minimization, 3. focusing only a few regions at a time, and 4. relying on stringent convergence criteria for high accuracy. Dumitras et al.86 proposed a three-step algorithm using angular-map-driven snakes for shape description and extraction of objects in color imagery. The first step involved computation of an angular map using all color pixel vectors and a reference vector that characterizes color changes in the input image. This map is utilized as input to an edge detection protocol in the second stage of processing. Finally, the resultant edge map is presented to a snake model to segment the object of interest. Dumitras et al. experimented with distance and GVF snake models in their work. The use of PAC evolution based on a cubic smoothing spline for real time segmentation of images was first seen in the work of Precioso et al.87 Moreover, through this work Precioso et al.87 demonstrated that the choice of a smoothing spline approximation instead of spline interpolation makes a snake more robust to noise variations. More recently, Ozertem et al.88 introduced a nonparametric formulation of a snake-energy function using kernel density estimation that exploited the underlying kernel density estimate of the image data. Lankton et al.89 propounded a method on region-based active contours driven by localized region energy calculations for improved segmentation accuracy. In comparison to PACs, GACs are implicitly represented in an Eulerian formulation where evolving curves are evaluated as the level sets of a distance function in two-dimensions, a theory first introduced for image segmentation by Malladi et al.90 based on the work originally done by Osher et al.91 The key idea of a level set-based segmentation method is to commence with a closed contour in two dimensions, which is eventually made to propagate in a direction orthogonal to itself at a specific speed , driven by a higher dimensional scalar function defined over the input image. Thus the evolving front at any location is derived as the zero level set of the aforementioned scalar function at time instant , mathematically represented as: Employing the chain rule on Eq. (7) and performing specific algebraic simplifications, the evolution of (given the value of ) can be expressed as: Equation (8) is popularly referred to as the level set equation and serves as a useful tool to track the evolution of contours along images. Figure 15 shows the segmentation results obtained using an open-source level set toolbox92 using default parametric settings. The primary virtue of GACs over alternate contour energy-based approaches is that its implicit boundary formulation can efficiently undergo topological changes pertinent to splitting or merging. Consequently GACs are better suited for shape-invariant multiregion/object segmentation. A secondary asset of GACs over conventional schemes is its nonparametric nature that allows it to be generically used for disparate datasets.Brox et al.93 designed a GAC-based segmentation approach for multiple regions utilizing coupled level set functions. More specifically, their segmentation framework employed one level set function for each region. It was novel because it allowed for the extraction of an arbitrary number of regions unlike conventional level set approaches that optimally extracted one or two regions. Michailovich et al.94 proposed a segmentation method for gray and color images based on GACs using an energy function that incorporated the Bhattacharya distance. The underlying algorithm was based on the notion that regions in an image can be delineated using a curve evolved in a manner such that the Bhattacharya distance between the estimates of probability densities among various segmentation classes is maximized. To this effect, a cost function that measured the dissimilarity between contents of regions was defined and employed such that a contour was made to converge to a shape that minimized overlap between the aforementioned contents (or equivalently maximized the distance among probability densities of various segments). Another approach targeted at segmenting multiple regions in color images using GACs was demonstrated in the work of Ayed et al.95 The proposed technique allowed the number of regions being segmented to be automatically varied via a region merging methodology Furthermore, Bertelli et al.96 employed GACs that evolved based on cost functions derived from within-region (pixel-pair) dissimilarity instead of between-region cuts in a binary or multiphase level set composition, for multiregion segmentation of color images. Xie97 introduced a GAC model that incorporated magnetostatic interactions among object boundaries and active contours for efficient segmentation. The proposed approach was found to be extremely robust in the presence of complex geometries as well as problems pertinent to contour initialization and weak/broken edges. The algorithm in Xie97 was enhanced in Xie,98 with and without random initializations of active contours, for object segmentation in color imagery. Fuzzy energy-based active contours using a pseudo-level set formulation for object detection/segmentation in color images was seen in the work by Krinidis et al.99 The advantages of their approach were, in general, twofold: 1. the underlying cost function was capable of detecting objects whose boundaries were not well defined by gradient calculations, and 2. the fuzzy energy alteration to the conventional model enabled a contour to quickly converge to the desired object of interest within a few iterations. Li et al.100 instituted a unique segmentation algorithm using GACs in a level set formulation wherein the regularity of the level set function was maintained during the curve evolution process. The approach was designed to minimize a cost function derived from gradient flow and was comprised of a distance regularization term in conjunction with an external energy term that forced the zero level set to the desired locations. On the other hand, Salah et al.101 introduced a process for multiregion segmentation of image data in a level set framework, using an energy functional that encompassed a term to evaluate the deviation of mapped data (acquired using a kernel function) within each segmented region from a piecewise model, in addition to a classic regularization term that enforced smoothness of region borders. More recently, Karoui et al.102 proposed an algorithm for segmentation of textured regions in images using a GAC-based level set formulation, which minimized a cost function comprised of a similarity measure between region features and texture descriptors, along with a boundary-based component that imposed smoothness/regularity of region boundaries on the evolution process. Ghosh et al.103 pioneered a single object segmentation algorithm in a variational formulation based on edge flow vectors derived from several image features pertaining to color, texture, and intensity edges. Wang et al.104 devised a color segmentation protocol based on the work by Deng et al.,65 using a level set formulation that minimized a global inhomogeneity metric for segmentation of photographic imagery. In context of GACs-based curve evolution, other notable contributions involved the use of Geodesic active contours for region/object segmentation. Geodesic active contours are dynamically modeled level set methods that facilitate combining common curve evolution practices with energy minimization techniques and are considered as the geometric alternative for snakes. In their work, Goldenberg et al.105 devised a computationally efficient implementation of a geodesic active contour model that was numerically consistent using a narrow band level set formulation and a fast marching technique. Their implementation, involving advanced numerical methods, was found to efficiently solve a geometric nonlinear model for applications involving region segmentation and object tracking. Furthermore, Sagiv et al.106 utilized a geodesic active contour framework for segmenting textured regions in natural scene images, where the texture was modeled using Gabor filters sensitive to a set of orientations, scales and frequencies. Mumford-Shah functional-based approachesChan et al.107 proposed a unique model for active contour-based segmentation using the Mumford-Shah (MS) functional. If , , and represent a smooth closed segmenting contour, the observed image data and its piece-wise approximation respectively, then the MS energy functional is defined as: In Eq. (9) symbolizes the image domain while the , , parameters appropriately weight various terms in the functional in order to control the segmentation scale and the smoothness of the outcome. The use of the MS functional enabled the development of a curve evolution process for region/object segmentation without utilizing edge information as a stopping criterion, as typically employed by conventional approaches. Tsai et al.108 extended the work of Chan et al.107 by divulging an estimation-theoretic approach to curve evolution using the MS functional for color image segmentation and smoothing. Heiler et al.109 proposed an algorithm for segmentation based on integrating the use of natural image statistics with the technique by Chan et al.107 In their work, Gao et al.110 demonstrated a new hierarchical image segmentation and smoothing algorithm based on a multiphase level set formulation and the Chan-Vese piecewise constant smooth active contour model. Bayesian segmentation techniquesA class of energy-based segmentation approaches that have maintained continued interest among researchers over the past few years stems from the field of probability theory wherein region characteristics are modeled through MRFs. In a standard MRF-based procedure, the segmentation objective is formulated using the maximum A-posteriori probability (MAP) criterion. According to the MAP criterion, a desired segmentation is defined as the one that maximizes the a posteriori probability of segmentation , pertaining to an observed image , which according to the Bayes rule is mathematically expressed as: The terms and are known as the class conditional and a priori probability distributions, respectively, while represents the set of all possible segmentation outcomes. The conditional probability is typically responsible for characterizing the underlying distribution of intensity values or other attributes/features in an image. In contrast, the a priori probability distribution is employed for imposing spatial connectivity constraints for region formation. Several optimization approaches [e.g., iterative conditional modes (ICM), highest confidence first (HCF), and simulated annealing] integrated with parametric estimation methods [e.g., expectation maximization (EM), maximum likelihood (ML) estimation] have been utilized to achieve the aforementioned maximization. The primary advantage of Bayesian-based segmentation is its mathematically principled approach that uses statistical inference and a priori information about the underlying data. Consequently it is extensively favored for segmenting images that contain nondeterministic content such as textures and statistical noise, which often prove challenging for traditional segmentation modus operandi. In his work, Mukherjee111 demonstrated an MRF-based algorithm that used a multidimensional luminance-chrominance feature space for improved segmentation of color images. The initial segmentation estimate for the MRF model was obtained using a conventional region growing approach, and the resultant regions were refined using a merging protocol. Gao et al.112 described a color image segmentation technique involving color conversion and MRF-EM modeling of regions in a unique narrow-band multiresolution implementation. The algorithm was initialized by a transformation of the input image from RGB to LUV for improved color differentiation, which was subsequently utilized as input to an MRF processing module. The parameters of the MRF model were estimated through an EM technique, wherein MRF-EM processing was invoked in a multiresolution framework for computational efficiency. Luo et al.113 introduced the concept of nonpurposive grouping (NPG) that defined the expectations of a perceptually acceptable segmentation outcome and proposed a probabilistic model to the NPG problem using an MRF formulation of regions in a HCF framework. Deng et al.114 evinced a function-based weighting parameter between the class conditional and the a priori probability components of an MRF model for image segmentation. The aforementioned weighting parameter was utilized to overcome the training phase typically necessitated to estimate MRF model parameters, consequently making the algorithm completely unsupervised. Tab et al.115 came up with a multiresolution color image segmentation approach, which was capable of segmenting regions with similar patterns across different resolution levels, by incorporating MRF modeling of regions and the discrete wavelet transform. The algorithm was specifically targeted at object-based wavelet coding applications. Xia et al.116 instituted an adaptive algorithm for segmenting textured images using a couple Markov random field (CMRF) comprised of a finite symmetric conditional Markov model (FSCM), which typified an image for feature extraction/estimation, and a multilevel logistic model (MLL), which characterized the labeling process to arrive at the desired segmentation outcome. The FSCM and MLL models were mutually dependent terms that were implemented using a simulated annealing scheme. Kato et al.117 pioneered an ICM-based architecture MRF model, which combined color and texture information for segmentation. Moreover, to facilitate accurate estimation of parameters requisited by the model, an estimation methodology based on the EM algorithm was developed. A couple of years later, Kato118 proposed a color image segmentation algorithm based on an MRF formulation in which pixel classes were characterized by a multivariate Gaussian distribution. Estimates of the number of classes, class model parameters, and pixel labels that made up the renowned “incomplete data problem” were all derived from a posterior distribution using a reversible jump Markov Chain Monte Carlo (RJMCMC) method. Diplaros et al.119 presented a novel generative model and EM algorithm for MRF-based color image segmentation that generated a class label for a pixel using prior distributions that shared similar parameters with its neighboring pixels. The proposed algorithm was found to possess an advantage of being relatively simple from an implementation standpoint with competing qualitative performance against traditional MRF-based segmentation methods. Nikou et al.120 proposed a new family of Gauss-Markov random field (GMRF)-based smoothness priors for modeling class/label probability distributions needed in a conventional MRF using spatially variant finite mixture models (SVFMMs) for color image segmentation. An important aspect of the use of GMRFs in this work was that it took into account individual class statistics to enforce class-dependent smoothness constraints. More recently, the work by Nikou et al.120 was further used by Nikou et al.121 in 2010 to illustrate an advanced hierarchical Bayesian model for mixture model-based segmentation. Mignotte122 designed an MRF fusion model targeted at quickly integrating results estimated from multiple relatively simplistic clustering models to eventually yield an enhanced/accurate final segmentation. This work was novel in the fact that the MRF fusion model made use of a segmentation evaluation metric called the probabilistic rand index (PRI), wherein to have perceptual significance the fusion was achieved in the penalized maximum PRI sense. Chen et al.123 established a new segmentation algorithm formulated as a labeling problem using a probability maximization model, founded on an iterative optimization scheme that alternated between MAP and ML estimations. This MAP-ML-based technique was shown to qualitatively and quantitatively outperform state-of-the-art segmentation approaches. In their work, Vantaram et al.124 furnished a hybrid image segmentation algorithm using a Gibbs random field (GRF) model (which is an MRF formulation under specific constraints) to form an initial estimate of the label field. This estimate was subsequently refined using color, texture, and gradient features integrated with a split-and-merge mechanism to arrive at the final set of segmented regions (see Fig. 16 for sample outcomes using a default minimum segment size parameter ). Conditional random field (CRF), which is an extension of the conventional MRF model, is another probabilistic model that has been effectively used for segmentation. Zhang et al.125 devised an approach that combined a CRF to fashion spatial relationships among image superpixels with a multilayer Bayesian Network (BN) that sculpted casual dependencies pervasive among different image entities such as regions, edges vertices, to formulate a unified probabilistic graphical model for image segmentation. This unified graphical model was found to surpass the results obtained from prior art that explicitly employed either a CRF or BN for segmentation. On the other hand, Lee et al.126 proposed the use of the AdaBoost machine learning algorithm for identifying disparities between image regions in a CRF formulation for efficient segmentation in automatic/semi-automatic configurations. The approach was successfully demonstrated on document and natural scene type imagery. Similar to MRFs, a popular category of Bayesian segmentation methods that originate from the field of probability theory are the ones based on Gaussian mixture models (GMMs) for representing region processes in images. Carson et al.127 proposed an image segmentation protocol wherein the joint distribution of color, texture, and position features were modeled as a mixture of Gaussians whose parameters were estimated using the EM algorithm. The resultant set of regions that Carson et al. called a “Blobworld” representation were employed in an image querying application with enhanced performance over classical content-based image retrieval procedures. In a similar architecture, Khan et al.128 presented an unsupervised color image segmentation algorithm where the joint distribution of pixel features pertinent to color, texture, brightness, and position were represented as GMMs. The underlying parameters for the models were assessed using three flavors of the EM algorithm namely penalized EM (PEM), penalized stochastic EM (PSEM) and a novel penalized inverse EM (PIEM) technique. The proposed PIEM method was tested on the Berkeley segmentation database with favorable performance. Integration of the mean shift algorithm and GMMs was first seen in the work by Park et al.,129 who developed a segmentation technique in which the number of mixture components were estimated using an adaptive mean shift methodology with parameters derived using a mean field annealing EM protocol. The aforementioned mean shift-GMM combination was found to be a competent solution for automatically segmenting color imagery without oversegmentation or isolated region formation. Greggio et al.130 instituted a fast GMM (FGMM)-based segmentation protocol that automatically inferred the number of components of a GMM as well as their corresponding means and covariances, without necessitating any prior knowledge or conscientious initialization. In contrast to some of the above-described GMM-based approaches, Liu et al.131 advocated the use of nonparametric mixture models with multivariate orthogonal polynomials to overcome the dependency of parametric models on a priori assumptions for color image segmentation. This methodology, named as the stochastic nonparametric EM (SNEM) technique, was evaluated on the Berkeley database and found to perform well in several empirical situations. Besides the energy-based techniques discussed in the last three subsections, several other approaches involving specialized energy classes,132 energy functionals,133,134 total variation (TV)-based functionals,135,136 convex relaxation procedures,137–139 curve evolution-based approaches,140–143 Bayesian principles 144–148 and other PDE as well as anisotropic diffusion-based techniques149–152 have been developed for various applications. Graph-based segmentation techniquesWithin the realms of energy-driven approaches, there exists a prominent category of techniques that employ graph representations for image segmentation. In a graph theoretic formulation (see Fig. 17), an image can be represented as an undirected graph , where every node corresponds to an individual pixel and every edge component pairwise connects neighboring pixel elements in , represented as vertices and . Additionally, each edge is assigned a weight () based on the amount of similarity between the two neighboring elements. Thus for an arbitrary image embodied as a graph, the ultimate goal from a segmentation viewpoint is to partition it utilizing metrics that yield a set of disconnected subgraphs exemplifying meaningful regions that concur with scene content. One significant benefit of graph-based approaches is their capitalization of various cost functions for global energy minimization that more often than not yield optimized segmentation outcomes in a generic framework. On the other hand, graph-partitioning methods suffer from significant computational complexity thereby requiring various restrictions and simplifications in order to yield reasonable results in practical real life applications at the expense of the quality of the segmentation. A popular criterion that involves identifying a set of edges crossing a specified path in a graph whose removal results in several disjoint subgraphs is generically called a “cut.” Furthermore, the aggregate weight of all the aforementioned edges that cross the cut is called its cost or capacity. It is imperative to understand that segmentation protocols using graphs are predominantly pair-wise graph partitioning processes that begin by splitting into two partitions and continue to recursively split subsequent subgroups until certain stopping criteria are met. Wu et al.153 was the first to demonstrate a novel spectral graph theoretic approach based on the minimum cut criterion for image segmentation. The algorithm was initiated by the construction of an adjacency graph analogous to the above-described architecture. Moreover, the weights () of the edge components were derived using a local derivative operator wherein large discontinuities (or strong edges) were associated with small costs while small discontinuities (or weak edges) were tagged with large costs. Subsequently, the proposed methodology determined the minimum cuts in the graph that collectively incurred the least cost during the partitioning process and in doing so identified closed contours comprised of strong edges in the scene as the final set of segments. A drawback of the minimum cut criterion was that it recurrently yielded small partitions containing isolated nodes in . To overcome this deficiency, Shi et al.154 proposed the normalized cut (Ncut) measure, which is an unbiased metric of disassociation between graph partitions. The Ncut criterion was computed as the cumulative ratio of, the aggregate weight of edge components crossing a cut to the aggregate weight of edge components in various subgroups (that are delineated by a cut) connecting to all nodes in . To this effect, the Ncut value for isolated nodes was bound to be large, since the aggregate weight of edge components crossing a cut represents a large percentage of the total connections from that small set of isolated nodes to all other nodes in the graph. The introduction of the Ncut standard led to the development of several segmentation approaches.155,156 Malik et al.,155 devised a segmentation algorithm in a normalized cuts framework that incorporated contour cues with texture features based on the concept of textons, to facilitate formation of regions of consistent brightness and texture. On the other hand, Tao et al.156 established a robust color image segmentation algorithm that integrated the strengths of the mean shift and normalized cuts methodologies with real-time performance. In contrast to the Ncut solution that minimized the total linkage between partitions normalized by the association of the nodes within them, Sarkar et al.157 designed a segmentation algorithm based on an average cut metric that minimized the total link weight between partitions normalized by the size of the partitions. Sarkar et al.157 found the qualitative performance of the average cut criterion from a segmentation perspective to be similar to the Ncut measure with significantly reduced computational load. In their work, Gdalyahu et al.158 introduced a graph-based segmentation approach by defining a low complexity typical cut criterion robust to noise and spurious cluster formation. The algorithm is initiated by the formulation of samples cuts in generated using the Karger’s contraction algorithm to eventually derive an average solution called a typical cut for the optimal partitioning of . The work was demonstrated both on synthetic/real color and gray scale images. Wang et al.159 introduced an image segmentation algorithm that employed a cost function aimed at finding a cut with the minimum mean edge weight in a graph. The mean cut measure possessed several advantages over other graph-partitioning approaches as it facilitated cuts with open/closed contours, guaranteed connected partitions, and was not influenced by large foreground regions, smooth/short boundaries, and similar-weight partitions. A couple of years later, Wang et al.160 generalized their work in 2001 to define a revolutionary cost function for graph-based segmentation called the ratio cut that enabled region as well as pixel-based segmentation independent of size, shape, smoothness, and boundary-length attributes. Recently, Kim et al.161 proposed a novel approach for segmentation of color textured images by formulating the segmentation task as a minimum cut problem in a weighted graph, wherein information from color and texture features were fused in a multivariate mixture model. To find globally optimal minimum cuts, the unsupervised algorithm relied heavily on specific type of split moves. The graph-based mechanisms discussed thus far are fully automatic and require, in general, substantial computations. On the contrary, a significant effort has been devoted to the development of supervised techniques involving human interaction to overcome the computational burden manifested by their unsupervised counterparts as well as for achieving results that are more tailored towards user requirements. Boykov et al.162,163 proposed the first known interactive graph cuts-based segmentation algorithm designed to divide an image into foreground and background regions, as displayed in Fig. 18. To accomplish the aforementioned objective, Boykov et al. represented an image as an undirected graph where a node corresponded to a particular pixel and ascertained two additional nodes called an object terminal (source node-) and a background terminal (sink node-). In this new representation of , the set of edges consisted of two types of distinctly weighted components called neighborhood links (-links) that connected neighboring vertices ( and ), and terminal links (-links) that connected pixels to source/sink nodes. The algorithm starts by allowing a user, through mouse-operated brush strokes, to interactively mark a set of pixels (called “seeds”) pertaining to foreground/background content in the scene. These marked pixels were subsequently employed as hard constraints during the segmentation process. Additionally, the algorithm uses a cost function that incorporates region and boundary information imposed as soft constraints on the segmentation protocol. The aforementioned cost function was predicated on specific edge weights partially derived from foreground/background intensity histograms. Finally, a unique graph-cut framework based on the min-cut/max flow criterion164 was utilized to uncover a single globally optimal solution as the final segmentation outcome, satisfying user-defined hard constraints while maintaining the best balance between region and boundary information. The algorithm was demonstrated on gray scale images and 3-D CT/MRI volumes. Fig. 18Results of the interactive graph cuts-based segmentation algorithm in Boykov et al.,162 acquired using an implementation provided by Gulshan et al.165 Each image shown is user-defined foreground (white) and background (red) brush strokes as well as corresponding segmentation outcomes.  The work by Boykov et al.164 was further enhanced by Rother et al.,166 who devised an interactive graph-cut methodology for color imagery called “GrabCut,” where color information was incorporated into the cost function using a Gaussian mixture model. The proposed technique first acquires an optimal “hard” partitioning result, using the aforementioned graph-cut algorithm enforced in an iterative scheme that fluctuates between estimation and parameter learning to solve the min-cut/max-flow criterion until convergence is achieved. Subsequently, a border matting protocol is employed as a post processing or corrective editing mechanism to arrive at the final segmentation result. Han et al.167 established a color image segmentation algorithm by extending the GrabCut methodology to accommodate color and multiscale nonlinear structure tensor texture (MSNST) features. This augmented GrabCut technique was found to have superior performance in comparison with its traditional equivalent over a diverse test bed of images taken from the Berkeley segmentation database. Li et al.168 developed an interactive foreground/background segmentation tool called “Lazy Snapping” with instant visual feedback driven by a novel segmentation algorithm that integrated graph cuts and precomputed oversegmentation. The proposed framework comprised of an object-marking step where users indicate foreground objects of interest at a coarse scale, followed by a boundary-editing step where object boundaries are delineated at a finer scale. Yang et al.169 devised a new foreground/background segmentation algorithm called “progressive-cut” that explicitly incorporated user evaluation and interaction, along with intention/expectation in a graph-cut schema, for yielding enhanced visual feedback and segmentation accuracy with minimal interaction. Feng et al.170 proposed an unsupervised extension of the binary (or foreground/background) graph cut known as a graduated graph cut (GGC), with an architecture that possessed capabilities of self-validated labeling of MRFs. Moreover, by utilizing different MRF optimizing protocols, Feng et al. proposed three algorithms; namely, tree-structured graph cuts (TSGC), net structured graph cuts (NSGC), and hierarchical graph cuts (HGC) for color image segmentation. Among other advancements concerned with graph-based segmentation, a number of approaches have been developed that fall outside the category of using “cuts” for partitioning an image. Felzenszwalb et al.171 developed a tree-structured segmentation technique by defining a predicate for determining the existence of a boundary pairwise between regions, utilizing graph representations of images (see Fig. 19). This predicate was defined as the disparity among pixel intensities along the boundary between the regions relative to the neighboring pixel intensity differences within each of the regions. The results portrayed in Fig. 19 were derived using default parametric settings , , and , each of which are illustrated in Felzenszwalb et al.171 Ding et al.172 established another tree-structured graph segmentation procedure for sematic object segmentation. The work employed a scale-based connected coherence tree algorithm (CCTA) that connected all coherent/similar pixels in a graph using a specific criterion that maximized the probability of them being part of salient regions in a scene. Dupuis et al.173 introduced a new color image segmentation process formulated in a graph-partitioning architecture where an affinity matrix, which signified the pairwise similarity of nodes (or pixels) in a graph, was acquired using a linear combination of affinity matrices from multiple visual cues such as color, texture, gradient, and luminance. The resultant affinity matrix was utilized in the partitioning process that included meta-edge computations and node contraction operations to arrive at the final segmentation result. Grady et al.174 proposed a graph-partitioning algorithm that uncovered partitions with small isoperimetric ratios, as an alternative to conventional spectral graph partitioning. The algorithm was found to be significantly faster in comparison to Ncuts-based segmentation with much more stable results. Image segmentation using random walks was first seen in the work of Grady175, who presented an interactive process, which assigned to every un-labeled pixel a label that corresponded to the highest probability that a random walker originating at that pixel would first reach the assigned label, from amongst a set of user-defined ones. The algorithm was demonstrated on synthetic and real imagery with satisfactory performance. The work in Grady et al.174 was extended by Yang et al.176 using a constrained random walk-based algorithm that accommodated multiple user inputs together with local contour deformation, for enabling highly accurate and computationally efficient object segmentation in color imagery. Xiang et al.177 designed an interactive image segmentation algorithm using graph-based transductive classification, a procedure that involved multiple linear reconstructions in small image windows (MLRW). The algorithm was a two-step process where, in every image window, the color intensity of the central pixel was first reconstructed using a weighted combination of its eight neighbors and the acquired optimal weights were in turn used in the second step to linearly reconstruct the class label of that pixel. Apart from the procedures discussed in this subsection, numerous supervised/unsupervised segmentation methods involving graph-cuts178–181 and hybrid techniques using graph formulations182–188 have been developed as tools for driving various imaging applications. Watershed-based segmentation techniquesOver the years, methods based on morphological watersheds have carved out a niche of their own in the segmentation literature. Watershed segmentation protocols typically utilize region as well as contour information to partition an image, by viewing it as a 3-D topographic relief (see Fig. 20) involving two spatial dimensions, and the third one being a specific attribute (e.g., intensity or gradient). Conceptually, watershed algorithms identify a pixel in an image as being stationed189 in the attribute-terrain, either within troughs/basins generally associated with region minimums or at a location where a drop of water would flow toward single or multiple region minimums. Pixel conglomerations that satisfy the first two conditions typically form catchment basins better known as watersheds, while ones that conform to the third condition (multiple region minimums) typify watershed lines, as depicted in Fig. 20. Watershed segmentation possesses several advantages such as: 1. simplicity in algorithmic design, 2. minimal computational complexity, 3. ability to provide close contours even in low contrast regions with weak boundaries, and 4. means to serve as a stable initialization for more sophisticated segmentation mechanisms. On the downside, the output achieved by a watershed transform is often oversegmented and requires post-processing schemes involving region merging and markers (connected components branding flat regions or objects in images) to yield a more suitable outcome. Gao et al.190 developed a three-step color image segmentation approach entailing simplification, marker extraction, and boundary decision processes, respectively. The first step was responsible for getting rid of any unwarranted image information from a segmentation standpoint, while the second step facilitated the functionality of homogeneous region identification. Finally, a modified region-growing-based watershed algorithm was performed in the last step to determine the eventual region boundaries. In a disparate research endeavor, Gao et al.191 devised a marker-based watershed segmentation methodology based on the concept of disjoint set union that involved pixel sorting, set union, and pixel resolving processes. Hill et al.192 incorporated the concept of texture gradient in a watershed segmentation framework to counter oversegmentation problems while partitioning textured regions that are perceptually homogeneous in images. The algorithm begins by extracting texture and gradient information from the scene using a nondecimated form for the complex wavelet transform. Subsequently, a new marker-guided watershed algorithm was employed to identify a final set of homogeneous textured/nontextured regions. Nguyen et al.193 pioneered a novel segmentation approach called “watersnakes” that unified principles from energy-based active contours with the watershed transform. Through the watersnake scheme, Nguyen et al. formulated watershed segmentation as an energy minimization problem for region/object segmentation. In a similar context of fusing energy-based methodologies and watershed segmentation, Vanhamel et al.194 utilized a vector energy-based nonlinear diffusion filtering multiscale space, where a hierarchy of strong edges, smooth segments, and detailed segments were extracted by color-gradient watersheds to identify meaningful regions. The aforementioned algorithm was demonstrated on simulated as well as natural scene color imagery. Kim et al.195 proposed an effective watershed segmentation method in a multiresolution architecture using a wavelet transform. Once the image pyramid was constructed, the algorithm starts at the lowest level using a watershed segmentation step. The obtained segments were optimized using a region-merging protocol and projected to the next higher resolution using an inverse wavelet transform. The aforesaid step was continued until a segmentation outcome at the highest/original image resolution was achieved. In contrast, Jung196 designed a color image segmentation protocol called Waveseg using a dyadic wavelet decomposition scheme to create multiresolution representations of the input image. To this effect, a watershed transformation was applied to the image at the lowest resolution yielding an initial segmentation. This segmentation estimate was repetitively projected to subsequent higher resolutions using inverse wavelet transforms and contour refinements processes to obtain a full resolution estimate of the identified regions. Finally, a region merging protocol was exercised to merge adjoining regions with similar colors producing the output segmentation result. The algorithm was found to perform favorably in comparison to state-of-the-art methods especially when handling noisy color images. Arbeláez et al.197 introduced a three-step contemporary image segmentation strategy (abbreviated as ) involving a transformation, called the oriented watershed transform (OWT). In the first step, the proposed algorithm detects contours in the input image by computing a metric called the globalized probability of boundary (), using brightness, color, and texture cues. The identified contours (which may not be closed) are subsequently given as input to an OWT to yield an initial set of regions. Finally, an agglomerative clustering procedure is utilized to hierarchically form meaningful regions represented as a “region-tree” by an ultrametric contour map (UCM). Figure 21 illustrates the results of the methodology achieved by thresholding the UCM at level 0.3. In addition to the segmentation approaches discussed in this subsection, several other hybrid methods involving the watershed transform198,199 have been proposed, emphasizing its importance in the segmentation realm. As mentioned at the beginning of Sec. 2.2, a major portion of segmentation practices can be viewed as being either spatially blind or spatially guided, and within the notion of each of these principles, dominant groups of methods have been discussed. However, there are several techniques that may not distinctly fall in any of the aforementioned dominant categories but nonetheless provide valuable contributions to the field of image segmentation. Consequently, we will categorize them as a separate group called “miscellaneous” approaches. Among these are: 1. fuzzy-based procedures such as the ones involving fuzzy homogeneity200,201 and fuzzy region completion,202 2. supervised techniques using adaptive weighted distances,203 spline regression,204 geodesic matting,205 and linear programming,206 3. methods using specialized image features; namely, Quaternions,207,208 textons,209–212 histogram of oriented gradients (HOG),213 and local binary patterns (LBP)214,215 4. methodologies that employ turbo-pixel or super-pixel based representations of image data,216–221 5. physics-based processes robust to shadowing, shading, and highlighting effects222 (see Fig. 22 for sample segmentation outcomes with default parameters),223 6. routines that treat segmentation as a classification task using sophisticated classifiers such as support vector machines (SVMs)224,225 or employ specialized properties of images,226 7. top down (TD) or bottom up (BU) schemes using shape constraints, 227 as well as integrated TD-BU frameworks,228 8. mechanisms involving statistical principles,229 information bottleneck method230 and algorithms that consider segmentation as a task of finding perceptually salient groupings,231,232 and finally 9. co-clustering strategies, which combine multiple segmentations into one improved result233–235 as well as co-segmentation methods that jointly segment multiple images, which contain a common object.236–244 Co-clustering and co-segmentation (referenced above) are amongst the newest techniques being researched in the segmentation domain. Co-clustering is formally defined as the process of jointly clustering two or more images that closely maintain their semantic foreground and background content such as shapes, color, and texture of objects/regions. Examples of such a set of images include digital video frames in close proximity and series of images taken under varying camera exposure and/or illumination conditions. On the other hand, co-segmentation is a procedure wherein multiple images that have diverse backgrounds are processed to segment common foreground objects well correlated in terms of their color-texture composition. Co-segmentation has several applications such as image editing, image similarity measurement, video summarization/tracking, and object-based image retrieval to name a few. 3.Quantitave Evaluation of Segmentation MethodologiesThe unprecedented growth in the number of applications involving segmentation across diverse imaging modalities has resulted in the development of metrics for quantitative evaluation of segmentation methods and their corresponding outcomes. In his work, Zhang245 provided a comprehensive review of approaches established to analyze segmentations from a quantitative viewpoint that categorized most approaches as being either analytical or empirical based on their fundamental principle of operation. While the techniques in the analytical category typically grade segmentations by analyzing properties of the algorithms that generated them, empirical techniques indirectly gauge segmentation quality by using test images that have reference/ground truth results to compute consistency and/or discrepancy metrics between them. In order to objectively judge the quality of various segmentation outcomes displayed in this paper, we adopt an empirical/indirect evaluation technique utilizing a metric called the normalized probabilistic rand (NPR) index.246 The NPR index is an accurate measure of segmentation correctness that satisfies the following properties: 1. it does not yield high values in cases where there is significant discrepancy between an automatically generated (or test) segmentation result and the ones partitioned by human observers, 2. it does not make any label assignment and region size assumptions within the data being evaluated, 3. it accommodates lesser penalty for disagreement between a test segmentation outcome and its multiple manually generated counterparts in perceptually ambiguous regions, while it effects a heavy penalty for nonconformity in perceptually distinct regions, and 4. it yields intelligible comparisons between segmentations of different images and different segmentations of the same image. The NPR index is a normalized version of the probabilistic rand (PR) index, which in turn is formulated from the rand index ().247 If and are two segmentations being compared (test versus ground truth), then is defined as the ratio of number of pixel-pairs that share the same label relationship between them, represented as: In Eq. (11) denotes the number of pixels in and with corresponding label assignments and respectively, symbolizes an identity function, ‘^’ represents a logical conjunction, while the denominator represents all possible unique pixel pair combinations with pixels. From the definition of , it can be seen that the metric is capable of performing only one-to-one test versus ground truth segmentation comparisons. On the other hand, the probabilistic rand () index allows comparison of one-test segmentation () to many ground truths () via a nonuniform pixel pair weighting scheme hinged on the variability in the ground-truth set. Thus if , , respectively represent the label assignment of a pixel (where ) in and the k’th manual segmentation (), while denote the set of “true labels” for , then is defined as: where and signify the respective probabilities of an identical or distinct label relationship between a pixel pair , obtained as:It is imperative to note that both the and PR indices range from 0 to 1, where 0 signifies complete dissimilarity, and 1 represents a perfect match with single/multiple ground truths. However this range () has often been found to be too narrow for comparison of a large set of images and also does not facilitate comparison of segmentations of different images. To this effect, Unnikrishnan et al.246 proposed the normalized probabilistic rand (NPR) index, which is referenced with respect to expected value of the PR index , defined as: where , while is computed as:If an arbitrary test database comprises of images each possessing number of ground truths, then and are computed as: From Eqs. (16) to (17), it can be observed that and are procured from all unordered pixel pairs across the entire set of ground truth segmentations of the test database, yielding a meaningful calculation of . Furthermore, from Eq. (15) it can be inferred that a segmentation output that possesses a PR value less than will yield a negative NPR value indicating a poor outcome, while segmentations associated with positive NPR values that are notably greater than zero () are considered useful. This negative to positive range of NPR values renders the index to be a significantly more sensitive and robust metric in comparison to PR. Figure 23 illustrates a distributional comparison of NPR scores for 11 different segmentation algorithms (see Fig. 23 legend) discussed earlier. These were tested on an open source database provided by the University of California at Berkeley comprising of 300 images cumulatively associated with 1,633 ground truth segmentations.1 It should be noted that the calculated value of the expected index [see Eqs. (16) to (18)] that was utilized to compute the NPR index [see Eq. (15)] was found to be equal to 0.6064. Additionally, a summary of our evaluation results for the aforementioned algorithms can be found in Table 1. Table 1Quantitative evaluation of segmentation results.
From Fig. 23 it can be observed that among the various methodologies that were evaluated, the distributions of the UCM, GSEG, MAPGSEG, and GRF methods are weighted more toward the right half of the bar graph in comparison to others, indicating superior performance. This observation can be corroborated by the results in Table 1 that depicts that the four aforementioned algorithms have the highest average NPR indices (0.507, 0.496, 0.495, 0.488, respectively) with the lowest deviation in NPR scores (0.322, 0.306, 0.312, 0.309), as well as the largest number of images in the range (105, 91, 85, 83) all of which indicate that these algorithms have the best segmentation performance with high consistency. 4.ConclusionsIn this paper, we present an extensive review of recent color segmentation methodologies and highlight prominent contributions in the gray scale realm. Our classification of segmentation approaches fundamentally involves two dominant groups: 1. spatially blind methods that entirely disregard spatial information, and 2. spatially guided techniques that employ information derived from the spatial distribution of pixels. Furthermore, the aforesaid classification is not “hard,” owing to the fact that there are a numerous techniques that, in some respect, integrate spatially blind processing with information that is spatially derived or vice versa, consequently fuzzifying the demarcation between them. This fuzzy nature may also be observed within subgroups of the segmentation hierarchy described in Fig. 3. Nonetheless, we have ensured that all algorithms have been placed in a group/subgroup to which they are most relevant. Overall, our perspective of the field, based on methods discussed in this paper, have led us to make the following observations: 1. segmentation continues to be at the forefront of many commercial and research endeavors, and the need for algorithms that perform this task efficiently is exponentially increasing with no sign of subsiding in the near future, 2. among various procedures developed within the last decade, energy-driven schemes involving active contours, Bayesian principles and graph partitioning techniques have received considerable attention relative to other mechanisms, and 3. in contrast to the 1990s, modern segmentation approaches have successfully managed to achieve higher levels of sophistication and quality, due to increased efforts to develop algorithms that combine the strengths of multiple processes to overcome existing drawbacks. While all our observations allude to advances that have been made in the area of image segmentation, we believe there are still significant contributions that have yet to be made. First, the bounty of segmentation methods has resulted in an increased requirement of supervised/unsupervised performance evaluation methodologies. Although the development of evaluation strategies has been the focus of several research undertakings, it has not been proportionate to the number of algorithms established to perform the task itself. This provides an opportunity for improvement as well as opens new avenues of research such as integration of segmentation and evaluation. It is our conviction that since segmentation is an ill-posed problem with no perfect solution, the ultimate algorithm will be one that eventually performs segmentation and evaluation in an adaptive feedback mechanism, in order to define an optimal or a generally acceptable solution. Second, enormous technological strides have been made in simultaneous capture/representation of data derived from multiple modalities of imaging (such as a co-registered RGB-hyperspectral-LIDAR (light detection and ranging) dataset of a scene or CT-MRI-PET data of a medical study), as different modalities provide different levels and type of information. However, segmentation techniques that successfully leverage information manifested in these enhanced formats are relatively few in comparison. To this effect, we believe that the next generation of segmentation algorithms should be developed with a multi-modal perspective to simultaneously cater to the requirements of sophisticated applications that employ such data sets whilst being backward compatible with applications using gray scale or color imagery. AcknowledgmentsThis work was supported by the Chester F. Carlson Center for Imaging Science and the Department of Electrical and Microelectronic Engineering, Rochester Institute of Technology, Rochester, NY. We would like to thank the authors of Christoudias et al.,18 Yang et al.,43 Deng et al.,65 Felzenszwalb et al.,171 Arbeláez et al.,197 Hoang et al.,222 Sumengen,92 Gulshan et al.,165 for providing source codes and/or results of their respective segmentation algorithms as well as the anonymous reviewers for their valuable comments. ReferencesD. Martinet al.,
“A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics,”
in 8th IEEE Inter. Conf. Comp. Vis. (ICCV),
416
–423
(2001). Google Scholar
K. S. FuJ. K. Mui,
“A survey on image segmentation,”
Elsevier Pattern Recogn., 13
(1), 3
–16
(1981). http://dx.doi.org/10.1016/0031-3203(81)90028-5 PTNRA8 0031-3203 Google Scholar
N. R. PalS. K. Pal,
“A review on image segmentation techniques,”
Elsevier Pattern Recogn., 26
(9), 1277
–1294
(1993). http://dx.doi.org/10.1016/0031-3203(93)90135-J PTNRA8 0031-3203 Google Scholar
L. LuccheseS. K. Mitra,
“Color image segmentation: a state-of-the-art survey,”
Proc. Indian Natl. Sci. Acad., 67
(2), 207
–221
(2001). PIPSBD 0370-0046 Google Scholar
H. D. Chenget al.,
“Color image segmentation: advances & prospects,”
Pattern. Recogn. Soc., 34
(12), 2259
–2281
(2001). http://dx.doi.org/10.1016/S0031-3203(00)00149-7 PTNRA8 0031-3203 Google Scholar
P. GreenL. MacDonald, Color Engineering, John Wiley and Sons Ltd., Hoboken, New Jersey
(2002). Google Scholar
P. A. ArbeláezL. D. Cohen,
“A metric approach to vector-valued image segmentation,”
Int. J. Comp. Vis., 69
(1), 119
–126
(2006). http://dx.doi.org/10.1007/s11263-006-6857-5 IJCVEQ 0920-5691 Google Scholar
J. WangL. JuX. Wang,
“An edge-weighted centroidal voronoi tessellation model for image segmentation,”
IEEE Trans. Image Proc., 18
(8), 1844
–1858
(2009). http://dx.doi.org/10.1109/TIP.2009.2021087 IIPRE4 1057-7149 Google Scholar
J. McQueen,
“Some methods for classification and analysis of multivariate observations,”
in Proc. 5th Berkeley Symp. Math. Statist. Prob.,
281
–296
(1967). Google Scholar
T. Kanungoet al.,
“An efficient k-means clustering algorithm: analysis and implementation,”
IEEE Trans. Pattern Anal. Mac. Intel., 24
(7), 881
–892
(2002). http://dx.doi.org/10.1109/TPAMI.2002.1017616 ITPIDJ 0162-8828 Google Scholar
J. Chenet al.,
“Adaptive perceptual color-texture image segmentation,”
IEEE Trans. Image Proc., 14
(10), 1524
–1536
(2005). http://dx.doi.org/10.1109/TIP.2005.852204 IIPRE4 1057-7149 Google Scholar
M. Mignotte,
“Segmentation by fusion of histogram-based k-means clusters in different color spaces,”
IEEE Trans. Image Proc., 17
(5), 780
–787
(2008). http://dx.doi.org/10.1109/TIP.2008.920761 IIPRE4 1057-7149 Google Scholar
M. Mignotte,
“A de-texturing and spatially constrained k-means approach for image segmentation,”
Elsevier Pattern Recogn. Lett., 32
(2), 359
–367
(2011). http://dx.doi.org/10.1016/j.patrec.2010.09.016 PRLEDG 0167-8655 Google Scholar
Y. S. ChenB. T. ChenW. H. Hsu,
“Efficient fuzzy C-means clustering for image data,”
J. Electron. Imag., 14
(1), 013017
(2005). http://dx.doi.org/10.1117/1.1879012 JEIME5 1017-9909 Google Scholar
D. ComaniciuP. Meer,
“Mean shift: a robust approach toward feature space analysis,”
IEEE Trans. Pattern Anal. Mach. Intel., 24
(5), 603
–619
(2002). http://dx.doi.org/10.1109/34.1000236 ITPIDJ 0162-8828 Google Scholar
K. FukunagaL. D. Hosteler,
“The estimation of the gradient of a density function, with applications in pattern recognition,”
IEEE Trans. Inform. Theor., 21
(1), 32
–40
(1975). http://dx.doi.org/10.1109/TIT.1975.1055330 IETTAW 0018-9448 Google Scholar
Y. Cheng,
“Mean shift, mode seeking, and clustering,”
IEEE Trans. Pattern Anal. Mach. Intel., 17
(8), 790
–799
(1995). http://dx.doi.org/10.1109/34.400568 ITPIDJ 0162-8828 Google Scholar
C. M. ChristoudiasB. GeorgescuP. Meer,
“Synergism in low-level vision,”
in 16th IEEE Int. Conf. Pattern Recogn.,
150
–155
(2002). Google Scholar
Y. HongJ. YiD. Zhao,
“Improved mean shift segmentation approach for natural images,”
Appl. Math. Comput., 185
(2), 940
–952
(2007). http://dx.doi.org/10.1016/j.amc.2006.07.038 AMHCBQ 0096-3003 Google Scholar
M. OzdenE. Polat,
“A color image segmentation approach for content-based image retrieval,”
Elsevier Pattern Recogn., 40
(4), 1318
–1325
(2007). http://dx.doi.org/10.1016/j.patcog.2006.08.013 PTNRA8 0031-3203 Google Scholar
T. Kohonen,
“The self-organizing map,”
Proc. IEEE, 78
(9), 1464
–1480
(1990). http://dx.doi.org/10.1109/5.58325 IEEPAD 0018-9219 Google Scholar
H. Y. HuangY. S. ChenW. H. Hsu,
“Color image segmentation using a self-organizing map algorithm,”
J. Electron. Imag., 11
(2), 136
–148
(2002). http://dx.doi.org/10.1117/1.1455007 JEIME5 1017-9909 Google Scholar
S. H. Onget al.,
“Segmentation of color images using a two-stage self-organizing network,”
Elsevier Image Vis. Comp., 20
(4), 279
–289
(2002). http://dx.doi.org/10.1016/S0262-8856(02)00021-5 IVCODK 0262-8856 Google Scholar
N. LiY. F. Li,
“Feature encoding for unsupervised segmentation of color images,”
IEEE Trans. Syst. Man Cyber. B, 33
(3), 438
–447
(2003). http://dx.doi.org/10.1109/TSMCB.2003.811120 ITSCFI 1083-4419 Google Scholar
G. DongM. Xie,
“Color clustering and learning for image segmentation based on neural networks,”
IEEE Trans. Neural Networks, 16
(4), 925
–936
(2005). http://dx.doi.org/10.1109/TNN.2005.849822 ITNNEP 1045-9227 Google Scholar
N. C. Yeoet al.,
“Colour image segmentation using the self-organizing map and adaptive resonance theory,”
Elsevier Image Vis. Comp., 23
(12), 1060
–1079
(2005). http://dx.doi.org/10.1016/j.imavis.2005.07.008 IVCODK 0262-8856 Google Scholar
A. R. F. AraújoD. C. Costa,
“Local adaptive receptive field self-organizing map for image color segmentation,”
Elsevier Image Vis. Comp., 27
(9), 1229
–1239
(2009). http://dx.doi.org/10.1016/j.imavis.2008.11.014 IVCODK 0262-8856 Google Scholar
A. S. Frisch,
“Unsupervised construction of fuzzy measures through self-organizing feature maps and its application in color image segmentation,”
Elsevier Inter. J. Approx. Reason., 41
(1), 23
–42
(2006). http://dx.doi.org/10.1016/j.ijar.2005.06.020 IJARE4 0888-613X Google Scholar
D. E. IleaP. F. Whelan,
“CTex—an adaptive unsupervised segmentation algorithm based on color-texture coherence,”
IEEE Trans. Image Proc., 17
(10), 1926
–1939
(2008). http://dx.doi.org/10.1109/TIP.2008.2001047 IIPRE4 1057-7149 Google Scholar
J. C. Dunn,
“A fuzzy relative of the ISODATA process and its use in detecting compact well-separated clusters,”
J. Cybernetics, 3
(3), 32
–57
(1973). http://dx.doi.org/10.1080/01969727308546046 JCYBAY 0022-0280 Google Scholar
J. F. YangS. S. HaoP. C. Chung,
“Color image segmentation using fuzzy C-means and eigenspace projections,”
Elsevier Sign. Proc., 82
(3), 461
–472
(2002). http://dx.doi.org/10.1016/S0165-1684(01)00196-7 SPRODR 0165-1684 Google Scholar
A. W. C. LiewH. YanN. F. Law,
“Image segmentation based on adaptive cluster prototype estimation,”
IEEE Trans. Fuzzy Sys., 13
(4), 444
–453
(2005). http://dx.doi.org/10.1109/TFUZZ.2004.841748 IEFSEV 1063-6706 Google Scholar
W. L. HungM. S. YangD. H. Chen,
“Bootstrapping approach to feature-weight selection in fuzzy C-means algorithms with an application in color image segmentation,”
Elsevier Pattern Recogn. Lett., 29
(9), 1317
–1325
(2008). http://dx.doi.org/10.1016/j.patrec.2008.02.003 PRLEDG 0167-8655 Google Scholar
I. Tziakoset al.,
“Color image segmentation using laplacian eigenmaps,”
J. Electron. Imag., 18
(2), 023004
(2009). http://dx.doi.org/10.1117/1.3122369 JEIME5 1017-9909 Google Scholar
S. KrinidisV. Chatzis,
“A robust fuzzy local information C-means clustering algorithm,”
IEEE Trans. Image Proc., 19
(5), 1328
–1337
(2010). http://dx.doi.org/10.1109/TIP.2010.2040763 IIPRE4 1057-7149 Google Scholar
X. Y. WangJ. Bu,
“A fast and robust image segmentation using FCM with spatial information,”
Elsevier Dig. Sign. Proc., 20
(4), 1173
–1182
(2010). http://dx.doi.org/10.1016/j.dsp.2009.11.007 DSPREJ 1051-2004 Google Scholar
Z. Yuet al.,
“An adaptive unsupervised approach toward pixel clustering and color image segmentation,”
Elsevier Pattern Recogn., 43
(5), 1889
–1906
(2010). http://dx.doi.org/10.1016/j.patcog.2009.11.015 PTNRA8 0031-3203 Google Scholar
C. J. VeenmanM. J. T. ReindersE. Backer,
“A cellular coevolutionary algorithm for image segmentation,”
IEEE Trans. Image Proc., 12
(3), 304
–316
(2003). http://dx.doi.org/10.1109/TIP.2002.806256 IIPRE4 1057-7149 Google Scholar
M. S. Alliliet al.,
“Image and video segmentation by combining unsupervised generalized gaussian mixture modeling and feature selection,”
IEEE Trans. Circ. Syst. Video Tech., 20
(10), 1373
–1377
(2010). http://dx.doi.org/10.1109/TCSVT.2010.2077483 ITCTEM 1051-8215 Google Scholar
B. K. JeonY. B. JungK. S. Hong,
“Image segmentation by unsupervised sparse clustering,”
Elsevier Pattern Recogn. Lett., 27
(14), 1650
–1664
(2006). http://dx.doi.org/10.1016/j.patrec.2006.03.011 PRLEDG 0167-8655 Google Scholar
Z. A. AghbariR. A. Haj,
“Hill-manipulation: an effective algorithm for color image segmentation,”
Elsevier Image Vis. Comp., 24
(8), 894
–903
(2006). http://dx.doi.org/10.1016/j.imavis.2006.02.013 IVCODK 0262-8856 Google Scholar
Y. Maet al.,
“Segmentation of multivariate mixed data via lossy data coding and compression,”
IEEE Trans. Pattern Anal. Mach. Intel., 29
(9), 1546
–1562
(2007). http://dx.doi.org/10.1109/TPAMI.2007.1085 ITPIDJ 0162-8828 Google Scholar
A. Y. Yanget al.,
“Unsupervised segmentation of natural images via lossy data compression,”
Elsevier Comp. Vis. Image Understanding, 110
(2), 212
–225
(2008). http://dx.doi.org/10.1016/j.cviu.2007.07.005 CVIUF4 1077-3142 Google Scholar
R. Huanget al.,
“Image segmentation via coherent clustering in color space,”
Elsevier Pattern Recogn. Lett., 32
(7), 891
–902
(2011). http://dx.doi.org/10.1016/j.patrec.2011.01.013 PRLEDG 0167-8655 Google Scholar
M. SezginB. Sankur,
“Survey over image thresholding techniques and quantitative performance evaluation,”
J. Elec. Imag., 13
(1), 146
–165
(2004). http://dx.doi.org/10.1117/1.1631315 JEIME5 1017-9909 Google Scholar
K. U. Barthel,
“3D-data representation with ImageJ,”
in ImageJ User and Developer Conf.,
(2006). Google Scholar
F. KurugolluB. SankurA. E. Harmanci,
“Color image segmentation using histogram multithresholding and fusion,”
Elsevier Image Vis. Comp., 19
(13), 915
–928
(2001). http://dx.doi.org/10.1016/S0262-8856(01)00052-X IVCODK 0262-8856 Google Scholar
H. D. ChengX. H. JiangJ. Wang,
“Color image segmentation based on homogram thresholding and region merging,”
Elsevier Pattern Recogn., 35
(2), 373
–393
(2002). http://dx.doi.org/10.1016/S0031-3203(01)00054-1 PTNRA8 0031-3203 Google Scholar
M. M. MushrifA. K. Ray,
“Color image segmentation: rough-set theoretic approach,”
Elsevier Pattern Recogn. Lett., 29
(4), 483
–493
(2008). http://dx.doi.org/10.1016/j.patrec.2007.10.026 PRLEDG 0167-8655 Google Scholar
M. M. MushrifA. K. Ray,
“A-IFS histon based multithresholding algorithm for color image segmentation,”
IEEE Sign. Proc. Lett., 16
(3), 168
–171
(2009). http://dx.doi.org/10.1109/LSP.2008.2010820 IESPEJ 1070-9908 Google Scholar
S. ManayA. Yezzi,
“Anti-geometric diffusion for adaptive thresholding and fast segmentation,”
IEEE Trans. Image Proc., 12
(11), 1310
–1323
(2003). http://dx.doi.org/10.1109/TIP.2003.818039 IIPRE4 1057-7149 Google Scholar
J. Fanet al.,
“Automatic image segmentation by integrating color-edge extraction and seeded region growing,”
IEEE Trans. Image Proc., 10
(10), 1454
–1466
(2001). http://dx.doi.org/10.1109/83.951532 IIPRE4 1057-7149 Google Scholar
S. Y. WanW. E. Higgins,
“Symmetric region growing,”
IEEE Trans. Image Proc., 12
(9), 1007
–1015
(2003). http://dx.doi.org/10.1109/TIP.2003.815258 IIPRE4 1057-7149 Google Scholar
I. FondónC. SerranoB. Acha,
“Color-texture image segmentation based on multistep region growing,”
Opt. Eng., 45
(5), 057002
(2006). http://dx.doi.org/10.1117/1.2205900 OPEGAR 0091-3286 Google Scholar
A. K. QinD. A. Clausi,
“Multivariate image segmentation using semantic region growing with adaptive edge penalty,”
IEEE Trans. Image Proc., 19
(8), 2157
–2170
(2010). http://dx.doi.org/10.1109/TIP.2010.2045708 IIPRE4 1057-7149 Google Scholar
J. C. DevauxP. GoutonF. Truchetet,
“Karhunen-Loève transform applied to region-based segmentation of color aerial images,”
Opt. Eng., 40
(7), 1302
–1308
(2001). http://dx.doi.org/10.1117/1.1385166 OPEGAR 0091-3286 Google Scholar
H. C. ChenW. J. ChienS. J. Wang,
“Contrast-based color image segmentation,”
IEEE Sign. Proc. Lett., 11
(7), 641
–644
(2004). http://dx.doi.org/10.1109/LSP.2004.830116 IESPEJ 1070-9908 Google Scholar
R. NockF. Nielsen,
“Statistical region merging,”
IEEE Trans. Patt. Anal. Mach. Intel., 26
(11), 1452
–1458
(2004). http://dx.doi.org/10.1109/TPAMI.2004.110 ITPIDJ 0162-8828 Google Scholar
R. NockF. Nielsen,
“Semi-supervised statistical region refinement for color image segmentation,”
Elsevier Pattern Recogn., 38
(6), 835
–846
(2005). http://dx.doi.org/10.1016/j.patcog.2004.11.009 PTNRA8 0031-3203 Google Scholar
C. Kim,
“Segmenting a low-depth-of-field image using morphological filters and region merging,”
IEEE Trans. Image Proc., 14
(10), 1503
–1511
(2005). http://dx.doi.org/10.1109/TIP.2005.846030 IIPRE4 1057-7149 Google Scholar
Y. H. KuanC. M. KuoN. C. Yang,
“Color-based image salient region segmentation using novel region merging strategy,”
IEEE Trans. Multimedia, 10
(5), 832
–845
(2008). http://dx.doi.org/10.1109/TMM.2008.922853 ITMUF8 1520-9210 Google Scholar
Z. LiuL. ShenZ. Zhang,
“Unsupervised image segmentation based on analysis of binary partition tree for salient object extraction,”
Elsevier Sign. Proc., 91
(2), 290
–299
(2011). http://dx.doi.org/10.1016/j.sigpro.2010.07.006 SPRODR 0165-1684 Google Scholar
Z. TanN. H. C. Yung,
“Merging toward natural clusters,”
Opt. Eng., 48
(7), 077202
(2009). http://dx.doi.org/10.1117/1.3183892 OPEGAR 0091-3286 Google Scholar
F. CaldereroF. Marques,
“Region merging techniques using information theory statistical measures,”
IEEE Trans. Image Proc., 19
(6), 1567
–1586
(2010). http://dx.doi.org/10.1109/TIP.2010.2043008 IIPRE4 1057-7149 Google Scholar
Y. DengB. S. Manjunath,
“Unsupervised segmentation of color-texture regions in images and video,”
IEEE Trans. Pattern Anal. Mach. Intel., 23
(8), 800
–810
(2001). http://dx.doi.org/10.1109/34.946985 ITPIDJ 0162-8828 Google Scholar
Y. WangJ. YangN. Peng,
“Unsupervised color-texture segmentation based on soft criterion with adaptive mean-shift clustering,”
Elsevier Pattern Recogn. Lett., 27
(5), 386
–392
(2006). http://dx.doi.org/10.1016/j.patrec.2005.09.014 PRLEDG 0167-8655 Google Scholar
Y. G. WangJ. YangY. C. Chang,
“Color-texture image segmentation by integrating directional operators into JSEG method,”
Elsevier Pattern Recogn. Lett., 27
(16), 1983
–1990
(2006). http://dx.doi.org/10.1016/j.patrec.2006.05.010 PRLEDG 0167-8655 Google Scholar
S. C. Cheng,
“Region-growing approach to colour segmentation using 3-D clustering and relaxation labelling,”
Proc. IEEE Vis. Image Sign. Proc., 150
(4), 270
–276
(2003). http://dx.doi.org/10.1049/ip-vis:20030520 IVIPEK 1350-245X Google Scholar
F. Y. ShihS. Cheng,
“Automatic seeded region growing for color image segmentation,”
Elsevier Image Vis. Comp., 23
(10), 877
–886
(2005). http://dx.doi.org/10.1016/j.imavis.2005.05.015 IVCODK 0262-8856 Google Scholar
Y. HeY. LuoD. Hu,
“Automatic seeded region growing based on gradient vector flow for color image segmentation,”
Opt. Eng., 46
(4), 047003
(2007). http://dx.doi.org/10.1117/1.2724876 OPEGAR 0091-3286 Google Scholar
G. Balasubramanianet al.,
“Unsupervised color image segmentation using a dynamic color gradient thresholding algorithm,”
Proc. SPIE, 6806 68061H
(2008). http://dx.doi.org/10.1117/12.766184 Google Scholar
L. G. Ugarrizaet al.,
“Automatic image segmentation by dynamic region growth and multiresolution merging,”
IEEE Trans. Image Proc., 18
(10), 2275
–2288
(2009). http://dx.doi.org/10.1109/TIP.2009.2025555 IIPRE4 1057-7149 Google Scholar
S. R. Vantaramet al.,
“Multiresolution adaptive and progressive gradient-based color image SEGmentation,”
J. Elect. Imag., 19
(1), 013001
(2010). http://dx.doi.org/10.1117/1.3277150 JEIME5 1017-9909 Google Scholar
M. KrinidisI. Pitas,
“Color texture segmentation based on the modal energy of deformable surfaces,”
IEEE Trans. Image Proc., 18
(7), 1613
–1622
(2009). http://dx.doi.org/10.1109/TIP.2009.2018002 IIPRE4 1057-7149 Google Scholar
T. CelikT. Tjahjadi,
“Unsupervised colour image segmentation using dual-tree complex wavelet transform,”
Elsevier Comp. Vis. Image Understanding, 114
(7), 813
–826
(2010). http://dx.doi.org/10.1016/j.cviu.2010.03.002 CVIUF4 1077-3142 Google Scholar
C. PanagiotakisI. GriniasG. Tziritas,
“Natural image segmentation based on tree equipartition, bayesian flooding and region merging,”
IEEE Trans. Image Proc., 20
(8), 2276
–2287
(2011). http://dx.doi.org/10.1109/TIP.2011.2114893 IIPRE4 1057-7149 Google Scholar
S. SclaroffL. Liu,
“Deformable shape detection and description via model-based region grouping,”
IEEE Trans. Pattern Anal. Mach. Intel., 23
(5), 475
–489
(2001). http://dx.doi.org/10.1109/34.922706 ITPIDJ 0162-8828 Google Scholar
T. Gevers,
“Adaptive image segmentation by combining photometric invariant region and edge information,”
IEEE Trans. Pattern Anal. Mach. Intel., 24
(6), 848
–852
(2002). http://dx.doi.org/10.1109/TPAMI.2002.1008391 ITPIDJ 0162-8828 Google Scholar
E. NavonO. MillerA. Averbuch,
“Color image segmentation based on adaptive local thresholds,”
Elsevier Image Vis. Comp., 23
(1), 69
–85
(2005). http://dx.doi.org/10.1016/j.imavis.2004.05.011 IVCODK 0262-8856 Google Scholar
Q. LuoT. M. Khoshgoftaar,
“Unsupervised multiscale color image segmentation based on MDL principle,”
IEEE Trans. Image Proc., 15
(9), 2755
–2761
(2006). http://dx.doi.org/10.1109/TIP.2006.877342 IIPRE4 1057-7149 Google Scholar
L. PrasadA. N. Skourikhine,
“Vectorized image segmentation via trixel agglomeration,”
Elsevier Pattern Recogn., 39
(4), 501
–514
(2006). http://dx.doi.org/10.1016/j.patcog.2005.10.014 PTNRA8 0031-3203 Google Scholar
O. LézorayC. Charrier,
“Color image segmentation using morphological clustering and fusion with automatic scale selection,”
Elsevier Pattern Recogn. Lett., 30
(4), 397
–406
(2009). http://dx.doi.org/10.1016/j.patrec.2008.11.005 PRLEDG 0167-8655 Google Scholar
T. WanN. CanagarajahA. Achim,
“Segmentation of noisy colour images using cauchy distribution in the complex wavelet domain,”
IET Image Proc., 5
(2), 159
–170
(2011). http://dx.doi.org/10.1049/iet-ipr.2009.0300 1751-9659 Google Scholar
A. C. SobieranskiE. ComunelloA. V. Wangenheim,
“Learning a nonlinear distance metric for supervised region-merging image segmentation,”
Elsevier Comp. Vis. Image Understanding, 115
(2), 127
–139
(2011). http://dx.doi.org/10.1016/j.cviu.2010.09.006 CVIUF4 1077-3142 Google Scholar
M. KassA. WitkinD. Terzopoulos,
“Snakes: active contour models,”
Inter. J. Comp. Vis., 1
(4), 321
–331
(1988). http://dx.doi.org/10.1007/BF00133570 IJCVEQ 0920-5691 Google Scholar
A. DumitrasA. N. Venetsanopoulos,
“Angular map-driven snakes with application to object shape description in color images,”
IEEE Trans. Image Proc., 10
(12), 1851
–1859
(2001). http://dx.doi.org/10.1109/83.974570 IIPRE4 1057-7149 Google Scholar
F. Preciosoet al.,
“Robust real-time segmentation of images and videos using a smooth-spline snake-based algorithm,”
IEEE Trans. Image Proc., 14
(7), 910
–924
(2005). http://dx.doi.org/10.1109/TIP.2005.849307 IIPRE4 1057-7149 Google Scholar
U. OzertemD. Erdogmus,
“Nonparametric snakes,”
IEEE Trans. Image Proc., 16
(9), 2361
–2368
(2007). http://dx.doi.org/10.1109/TIP.2007.902335 IIPRE4 1057-7149 Google Scholar
S. LanktonA. Tannenbaum,
“Localizing region-based active contours,”
IEEE Trans. Image Proc., 17
(11), 2029
–2039
(2008). http://dx.doi.org/10.1109/TIP.2008.2004611 IIPRE4 1057-7149 Google Scholar
R. MalladiJ. A. SethianB. C. Vemuri,
“Shape modeling with front propagation: a level set approach,”
IEEE Trans. Pattern Anal. Mach. Intel., 17
(2), 158
–175
(1995). http://dx.doi.org/10.1109/34.368173 ITPIDJ 0162-8828 Google Scholar
S. OsherJ. A. Sethian,
“Fronts propagating with curvature-dependent speed: algorithms based on Hamilton-Jacobi formulations,”
J. Comput. Phys., 79
(1), 12
–49
(1988). http://dx.doi.org/10.1016/0021-9991(88)90002-2 JCTPAH 0021-9991 Google Scholar
B. Sumengen,
“A Matlab toolbox implementing level set methods,”
(2005) http://barissumengen.com/level_set_methods/ Google Scholar
T. BroxJ. Weickert,
“Level set segmentation with multiple regions,”
IEEE Trans. Image Proc., 15
(10), 3213
–3218
(2006). http://dx.doi.org/10.1109/TIP.2006.877481 IIPRE4 1057-7149 Google Scholar
O. MichailovichY. RathiA. Tannenbaum,
“Image segmentation using active contours driven by the Bhattacharyya gradient flow,”
IEEE Trans. Image Proc., 16
(11), 2787
–2801
(2007). http://dx.doi.org/10.1109/TIP.2007.908073 IIPRE4 1057-7149 Google Scholar
I. B. AyedA. Mitiche,
“A region merging prior for variational level set image segmentation,”
IEEE Trans. Image Proc., 17
(12), 2301
–2311
(2008). http://dx.doi.org/10.1109/TIP.2008.2006425 IIPRE4 1057-7149 Google Scholar
L. Bertelliet al.,
“A variational framework for multiregion pairwise-similarity-based image segmentation,”
IEEE Trans. Pattern Anal. Mach. Intel., 30
(8), 1400
–1414
(2008). http://dx.doi.org/10.1109/TPAMI.2007.70785 ITPIDJ 0162-8828 Google Scholar
X. XieM. Mirmehdi,
“MAC: magnetostatic active contour model,”
IEEE Trans. Pattern Anal. Mach. Intel., 30
(4), 632
–646
(2008). http://dx.doi.org/10.1109/TPAMI.2007.70737 ITPIDJ 0162-8828 Google Scholar
X. Xie,
“Active contouring based on gradient vector interaction and constrained level set diffusion,”
IEEE Trans. Image Proc., 19
(1), 154
–164
(2010). http://dx.doi.org/10.1109/TIP.2009.2032891 IIPRE4 1057-7149 Google Scholar
S. KrinidisV. Chatzis,
“Fuzzy energy-based active contours,”
IEEE Trans. Image Proc., 18
(12), 2747
–2755
(2009). http://dx.doi.org/10.1109/TIP.2009.2030468 IIPRE4 1057-7149 Google Scholar
C. Liet al.,
“Distance regularized level set evolution and its application to image segmentation,”
IEEE Trans. Image Proc., 19
(12), 3243
–3254
(2010). http://dx.doi.org/10.1109/TIP.2010.2069690 IIPRE4 1057-7149 Google Scholar
M. B. SalahA. MiticheI. B. Ayed,
“Effective level set image segmentation with a kernel induced data term,”
IEEE Trans. Image Proc., 19
(1), 220
–232
(2010). http://dx.doi.org/10.1109/TIP.2009.2032940 IIPRE4 1057-7149 Google Scholar
I. Karouiet al.,
“Variational region-based segmentation using multiple texture statistics,”
IEEE Trans. Image Proc., 19
(12), 3146
–3156
(2010). http://dx.doi.org/10.1109/TIP.2010.2071290 IIPRE4 1057-7149 Google Scholar
P. Ghoshet al.,
“A nonconservative flow field for robust variational image segmentation,”
IEEE Trans. Image Proc., 19
(2), 478
–490
(2010). http://dx.doi.org/10.1109/TIP.2009.2033983 IIPRE4 1057-7149 Google Scholar
W. WangR. Chung,
“Image segmentation by optimizing a homogeneity measure in a variational framework,”
J. Electron. Imag., 20
(1), 013009
(2011). http://dx.doi.org/10.1117/1.3543836 JEIME5 1017-9909 Google Scholar
R. Goldenberget al.,
“Fast geodesic active contours,”
IEEE Trans. Image Proc., 10
(10), 1467
–1475
(2001). http://dx.doi.org/10.1109/83.951533 IIPRE4 1057-7149 Google Scholar
C. SagivN. A. SochenY. Y. Zeevi,
“Integrated active—contours for texture segmentation,”
IEEE Trans. Image Proc., 15
(6), 1633
–1646
(2006). http://dx.doi.org/10.1109/TIP.2006.871133 IIPRE4 1057-7149 Google Scholar
T. F. ChanL. A. Vese,
“Active contours without edges,”
IEEE Trans. Image Proc., 10
(2), 266
–277
(2001). http://dx.doi.org/10.1109/83.902291 IIPRE4 1057-7149 Google Scholar
A. TsaiA. Yezzi Jr.A. S. Willsky,
“Curve evolution implementation of the Mumford-Shah functional for image segmentation, denoising, interpolation, and magnification,”
IEEE Trans. Image Proc., 10
(8), 1169
–1186
(2001). http://dx.doi.org/10.1109/83.935033 IIPRE4 1057-7149 Google Scholar
M. HeilerC. Schnorr,
“Natural image statistics for natural image segmentation,”
Inter. J. Comp. Vis., 63
(1), 5
–19
(2005). http://dx.doi.org/10.1007/s11263-005-4944-7 IJCVEQ 0920-5691 Google Scholar
S. GaoT. D. Bui,
“Image segmentation and selective smoothing by using Mumford-Shah model,”
IEEE Trans. Image Proc., 14
(10), 1537
–1549
(2005). http://dx.doi.org/10.1109/TIP.2005.852200 IIPRE4 1057-7149 Google Scholar
J. Mukherjee,
“MRF clustering for segmentation of color images,”
Elsevier Pattern Recogn. Lett., 23
(8), 917
–929
(2002). http://dx.doi.org/10.1016/S0167-8655(02)00022-3 PRLEDG 0167-8655 Google Scholar
J. GaoJ. ZhangM. G. Fleming,
“Novel technique for multiresolution color image segmentation,”
Opt. Eng., 41
(3), 608
–614
(2002). http://dx.doi.org/10.1117/1.1432315 OPEGAR 0091-3286 Google Scholar
J. LuoC. Guo,
“Perceptual grouping of segmented regions in color images,”
Elsevier Pattern Recogn., 36
(12), 2781
–2792
(2003). http://dx.doi.org/10.1016/S0031-3203(03)00170-5 PTNRA8 0031-3203 Google Scholar
H. DengD. A. Clausi,
“Unsupervised image segmentation using a simple MRF model with a new implementation scheme,”
Elsevier Pattern Recogn., 37
(12), 2323
–2335
(2004). http://dx.doi.org/10.1016/j.patcog.2004.04.015 PTNRA8 0031-3203 Google Scholar
F. A. TabG. NaghdyA. Mertins,
“Scalable multiresolution color image segmentation,”
Elsevier Sign. Proc., 86
(7), 1670
–1687
(2006). http://dx.doi.org/10.1016/j.sigpro.2005.09.016 SPRODR 0165-1684 Google Scholar
Y. XiaD. FengR. Zhao,
“Adaptive segmentation of textured images by using the coupled Markov random field model,”
IEEE Trans. Image Proc., 15
(11), 3559
–3566
(2006). http://dx.doi.org/10.1109/TIP.2006.877513 IIPRE4 1057-7149 Google Scholar
Z. KatoT. C. Pong,
“A Markov random field image segmentation model for color textured images,”
Elsevier Image Vis. Comp., 24
(10), 1103
–1114
(2006). http://dx.doi.org/10.1016/j.imavis.2006.03.005 IVCODK 0262-8856 Google Scholar
Z. Kato,
“Segmentation of color images via reversible jump MCMC sampling,”
Elsevier Image and Vis. Comp., 26
(3), 361
–371
(2008). http://dx.doi.org/10.1016/j.imavis.2006.12.004 IVCODK 0262-8856 Google Scholar
A. DiplarosN. VlassisT. Gevers,
“A spatially constrained generative model and an EM algorithm for image segmentation,”
IEEE Trans. Neural Networks, 18
(3), 798
–808
(2007). http://dx.doi.org/10.1109/TNN.2007.891190 ITNNEP 1045-9227 Google Scholar
C. NikouN. P. GalatsanosA. C. Likas,
“A class-adaptive spatially variant mixture model for image segmentation,”
IEEE Trans. Image Proc., 16
(4), 1121
–1130
(2007). http://dx.doi.org/10.1109/TIP.2007.891771 IIPRE4 1057-7149 Google Scholar
C. NikouA. C. LikasN. P. Galatsanos,
“A Bayesian framework for image segmentation with spatially varying mixtures,”
IEEE Trans. Image Proc., 19
(9), 2278
–2289
(2010). http://dx.doi.org/10.1109/TIP.2010.2047903 IIPRE4 1057-7149 Google Scholar
M. Mignotte,
“A label field fusion bayesian model and its penalized maximum rand estimator for image segmentation,”
IEEE Trans. Image Proc., 19
(6), 1610
–1624
(2010). http://dx.doi.org/10.1109/TIP.2010.2044965 IIPRE4 1057-7149 Google Scholar
S. Chenet al.,
“Image segmentation by MAP-ML estimations,”
IEEE Trans. Image Proc., 19
(9), 2254
–2264
(2010). http://dx.doi.org/10.1109/TIP.2010.2047164 IIPRE4 1057-7149 Google Scholar
S. R. VantaramE. Saber,
“An adaptive Bayesian clustering and multivariate region merging-based technique for efficient segmentation of color images,”
in IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP),
1077
–1080
(2011). Google Scholar
L. ZhangQ. Ji,
“Image segmentation with a unified graphical model,”
IEEE Trans. Pattern Anal. Mach. Intel., 32
(8), 1406
–1425
(2010). http://dx.doi.org/10.1109/TPAMI.2009.145 ITPIDJ 0162-8828 Google Scholar
S. H. LeeH. I. KooN. I. Cho,
“Image segmentation algorithms based on the machine learning of features,”
Elsevier Pattern Recogn. Lett., 31
(14), 2325
–2336
(2010). http://dx.doi.org/10.1016/j.patrec.2010.07.004 PRLEDG 0167-8655 Google Scholar
C. Carsonet al.,
“Blobworld: image segmentation using expectation-maximization and its application to image querying,”
IEEE Trans. Pattern Anal. Mach. Intel., 24
(8), 1026
–1038
(2002). http://dx.doi.org/10.1109/TPAMI.2002.1023800 ITPIDJ 0162-8828 Google Scholar
J. F. KhanR. R. AdhamiS. M. A. Bhuiyan,
“A customized gabor filter for unsupervised color image segmentation,”
Elsevier Image Vis. Comp., 27
(4), 489
–501
(2009). http://dx.doi.org/10.1016/j.imavis.2008.07.001 IVCODK 0262-8856 Google Scholar
J. H. ParkG. S. LeeS. Y. Park,
“Color image segmentation using adaptive mean shift and statistical model-based methods,”
Elsevier Comp. Math. App., 57
(6), 970
–980
(2009). http://dx.doi.org/10.1016/j.camwa.2008.10.053 MCMOEG 0895-7177 Google Scholar
N. Greggioet al.,
“Fast estimation of Gaussian mixture models for image segmentation,”
Mach. Vis. App., 23
(4), 773
–789
(2012). MVAPEO 0932-8092 Google Scholar
Z. Liuet al.,
“Color image segmentation using nonparametric mixture models with multivariate orthogonal polynomials,”
Neural Comp. App., 21
(4), 801
–811
(2012). 0941-0643 Google Scholar
P. A. ArbeláezL. D. Cohen,
“Energy partitions and image segmentation,”
J. Math. Imag. Vis., 20
(1–2), 43
–57
(2004). http://dx.doi.org/10.1023/B:JMIV.0000011318.77653.44 JIMVEC 0924-9907 Google Scholar
I. H. JermynH. Ishikawa,
“Globally optimal regions and boundaries as minimum ratio weight cycles,”
IEEE Trans. Pattern Anal. Mach. Intel., 23
(10), 1075
–1088
(2001). http://dx.doi.org/10.1109/34.954599 ITPIDJ 0162-8828 Google Scholar
T. SchoenemannS. MasnouD. Cremers,
“The elastic ratio: introducing curvature into ratio-based image segmentation,”
IEEE Trans. Image Proc., 20
(9), 2565
–2581
(2011). http://dx.doi.org/10.1109/TIP.2011.2118225 IIPRE4 1057-7149 Google Scholar
M. Ungeret al.,
“TVSeg—interactive total variation based image segmentation,”
in British Mach. Vis. Conf. (BMVC),
1
–10
(2008). Google Scholar
M. Donoseret al.,
“Saliency driven total variation segmentation,”
in 12th IEEE Inter. Conf. Comp. Vis. (ICCV),
817
–824
(2009). Google Scholar
T. Pocket al.,
“A convex relaxation approach for computing minimal partitions,”
in IEEE Inter. Conf. Comp. Vis. Pattern Recogn. (CVPR),
810
–817
(2009). Google Scholar
M. KlodtD. Cremers,
“A convex framework for image segmentation with moment constraints,”
in 13th IEEE Inter. Conf. Comp. Vis. (ICCV),
2236
–2243
(2011). Google Scholar
E. BrownT. ChanX. Bresson,
“Completely convex formulation of the Chan-Vese image segmentation model,”
Inter. J. Comp. Vis., 98
(1), 103
–121
(2012). http://dx.doi.org/10.1007/s11263-011-0499-y IJCVEQ 0920-5691 Google Scholar
M. S. AlliliD. Ziou,
“Globally adaptive region information for automatic color-texture image segmentation,”
Elsevier Pattern Recogn. Lett., 28
(15), 1946
–1956
(2007). http://dx.doi.org/10.1016/j.patrec.2007.05.002 PRLEDG 0167-8655 Google Scholar
A. AdamR. KimmelE. Rivlin,
“On scene segmentation and histograms-based curve evolution,”
IEEE Trans. Pattern Anal. Mach. Intel., 31
(9), 1708
–1714
(2009). http://dx.doi.org/10.1109/TPAMI.2009.21 ITPIDJ 0162-8828 Google Scholar
I. KokkinosG. EvangelopoulosP. Maragos,
“Texture analysis and segmentation using modulation features, generative models, and weighted curve evolution,”
IEEE Trans. Pattern Anal. Mach. Intel., 31
(1), 142
–157
(2009). http://dx.doi.org/10.1109/TPAMI.2008.33 ITPIDJ 0162-8828 Google Scholar
Z. LiJ. Fan,
“Stochastic contour approach for automatic image segmentation,”
J. Electron. Imag., 18
(4), 043004
(2009). http://dx.doi.org/10.1117/1.3257933 JEIME5 1017-9909 Google Scholar
Z. TuS. C. Zhu,
“Image segmentation by data-driven Markov chain Monte Carlo,”
IEEE Trans. Pattern Anal. Mach. Intel., 24
(5), 657
–673
(2002). http://dx.doi.org/10.1109/34.1000239 ITPIDJ 0162-8828 Google Scholar
B. C. KoH. Byun,
“FRIP: a region-based image retrieval tool using automatic image segmentation and stepwise Boolean and matching,”
IEEE Trans. Multimedia, 7
(1), 105
–113
(2005). http://dx.doi.org/10.1109/TMM.2004.840603 ITMUF8 1520-9210 Google Scholar
P. OrbanzJ. M. Buhmann,
“Nonparametric Bayesian image segmentation,”
Inter. J. Comp. Vis., 77
(1–3), 25
–45
(2008). http://dx.doi.org/10.1007/s11263-007-0061-0 IJCVEQ 0920-5691 Google Scholar
G. Scarpaet al.,
“Hierarchical multiple Markov chain model for unsupervised texture segmentation,”
IEEE Trans. Image Proc., 18
(8), 1830
–1843
(2009). http://dx.doi.org/10.1109/TIP.2009.2020534 IIPRE4 1057-7149 Google Scholar
L. ZhangQ. Ji,
“A Bayesian network model for automatic and interactive image segmentation,”
IEEE Trans. Image Proc., 20
(9), 2582
–2593
(2011). http://dx.doi.org/10.1109/TIP.2011.2121080 IIPRE4 1057-7149 Google Scholar
A. PetrovicO. D. EscodaP. Vandergheynst,
“Multiresolution segmentation of natural images: from linear to nonlinear scale-space representations,”
IEEE Trans. Image Proc., 13
(8), 1104
–1114
(2004). http://dx.doi.org/10.1109/TIP.2004.828431 IIPRE4 1057-7149 Google Scholar
X. DongI. Pollak,
“Multiscale segmentation with vector-valued nonlinear diffusions on arbitrary graphs,”
IEEE Trans. Image Proc., 15
(7), 1993
–2005
(2006). http://dx.doi.org/10.1109/TIP.2006.873473 IIPRE4 1057-7149 Google Scholar
A. SofouP. Maragos,
“Generalized flooding and multicue PDE-based image segmentation,”
IEEE Trans. Image Proc., 17
(3), 364
–376
(2008). http://dx.doi.org/10.1109/TIP.2007.916156 IIPRE4 1057-7149 Google Scholar
D. A. KayA. Tomasi,
“Color image segmentation by the vector-valued Allen-Cahn phase-field model: a multigrid solution,”
IEEE Trans. Image Proc., 18
(10), 2330
–2339
(2009). http://dx.doi.org/10.1109/TIP.2009.2026678 IIPRE4 1057-7149 Google Scholar
Z. WuR. Leahy,
“An optimal graph theoretic approach to data clustering: theory and Its application to image segmentation,”
IEEE Trans. Pattern Anal. Mach. Intel., 15
(11), 1101
–1113
(1993). http://dx.doi.org/10.1109/34.244673 ITPIDJ 0162-8828 Google Scholar
J. ShiJ. Malik,
“Normalized cuts and image segmentation,”
IEEE Trans. Pattern Anal. Mach. Intel., 22
(8), 888
–905
(2000). http://dx.doi.org/10.1109/34.868688 ITPIDJ 0162-8828 Google Scholar
J. Maliket al.,
“Contour and texture analysis for image segmentation,”
Inter. J. Comp. Vis., 43
(1), 7
–27
(2001). http://dx.doi.org/10.1023/A:1011174803800 IJCVEQ 0920-5691 Google Scholar
W. TaoH. JinY. Zhang,
“Color image segmentation based on mean shift and normalized cuts,”
IEEE Trans. Syst. Man Cyber. B, 37
(5), 1382
–1389
(2007). http://dx.doi.org/10.1109/TSMCB.2007.902249 ITSCFI 1083-4419 Google Scholar
S. SarkarP. Soundararajan,
“Supervised learning of large perceptual organization: graph spectral partitioning and learning automata,”
IEEE Trans. Pattern Anal. Mach. Intel., 22
(5), 504
–525
(2000). http://dx.doi.org/10.1109/34.857006 ITPIDJ 0162-8828 Google Scholar
Y. GdalyahuD. WeinshallM. Werman,
“Self-organization in vision: stochastic clustering for image segmentation, perceptual grouping, and image database organization,”
IEEE Trans. Pattern Anal. Mach. Intel., 23
(10), 1053
–1074
(2001). http://dx.doi.org/10.1109/34.954598 ITPIDJ 0162-8828 Google Scholar
S. WangJ. M. Siskind,
“Image segmentation with minimum mean cut,”
in 8th IEEE Inter. Conf. Comp. Vis. (ICCV),
517
–524
(2001). Google Scholar
S. WangJ. M. Siskind,
“Image segmentation with ratio cut,”
IEEE Trans. Pattern Anal. Mach. Intel., 25
(6), 675
–690
(2003). http://dx.doi.org/10.1109/TPAMI.2003.1201819 ITPIDJ 0162-8828 Google Scholar
J. S. KimK. S. Hong,
“Color texture segmentation using unsupervised graph cuts,”
Elsevier Pattern Recogn., 42
(5), 735
–750
(2009). http://dx.doi.org/10.1016/j.patcog.2008.09.031 PTNRA8 0031-3203 Google Scholar
Y. Y. BoykovM. P. Jolly,
“Interactive graph cuts for optimal boundary & region segmentation of objects in N-D Images,”
in 8th IEEE Inter. Conf. Comp. Vis. (ICCV),
105
–112
(2001). Google Scholar
Y. Y. BoykovG. F. Lea,
“Graph cuts and efficient N-D image segmentation,”
Inter. J. Comp. Vis., 70
(2), 109
–131
(2006). http://dx.doi.org/10.1007/s11263-006-7934-5 IJCVEQ 0920-5691 Google Scholar
Y. Y. BoykovV. Kolmogorov,
“An experimental comparison of min-cut/max-flow algorithms for energy minimization in vision,”
IEEE Trans. Pattern Anal. Mach. Intel., 26
(9), 1124
–1137
(2004). http://dx.doi.org/10.1109/TPAMI.2004.60 ITPIDJ 0162-8828 Google Scholar
V. Gulshanet al.,
“Geodesic star convexity for interactive image segmentation,”
(2010) http://www.robots.ox.ac.uk/~vgg/research/iseg/ Google Scholar
C. RotherV. KolmogorovA. Blake,
“GrabCut: interactive foreground extraction using iterated graph cuts,”
ACM Trans. Graphics (SIGGRAPH), 23
(3), 309
–314
(2004). Google Scholar
S. Hanet al.,
“Image segmentation based on grabcut framework integrating multiscale nonlinear structure tensor,”
IEEE Trans. Image Proc., 18
(10), 2289
–2302
(2009). http://dx.doi.org/10.1109/TIP.2009.2025560 IIPRE4 1057-7149 Google Scholar
Y. Liet al.,
“Lazy snapping,”
in ACM Trans. Graphics (SIGGRAPH),
303
–308
(2004). Google Scholar
Q. Yanget al.,
“Progressive cut: an image cutout algorithm that models user intentions,”
IEEE Multimedia, 14
(3), 56
–66
(2007). http://dx.doi.org/10.1109/MMUL.2007.60 IEMUE4 Google Scholar
W. FengJ. JiaZ. Q. Liu,
“Self-validated labeling of Markov random fields for image segmentation,”
IEEE Trans. Pattern Anal. Mach. Intel., 32
(10), 1871
–1887
(2010). http://dx.doi.org/10.1109/TPAMI.2010.24 ITPIDJ 0162-8828 Google Scholar
P. F. FelzenszwalbD. P. Huttenlocher,
“Efficient graph-based image segmentation,”
Inter. J. Comp. Vis., 59
(2), 167
–181
(2004). http://dx.doi.org/10.1023/B:VISI.0000022288.19776.77 IJCVEQ 0920-5691 Google Scholar
J. DingR. MaS. Chen,
“A scale-based connected coherence tree algorithm for image segmentation,”
IEEE Trans. Image Proc., 17
(2), 204
–216
(2008). http://dx.doi.org/10.1109/TIP.2007.912918 IIPRE4 1057-7149 Google Scholar
A. DupuisP. Vasseur,
“Image segmentation by cue selection and integration,”
Elsevier Image Vis. Comp., 24
(10), 1053
–1064
(2006). http://dx.doi.org/10.1016/j.imavis.2006.02.027 IVCODK 0262-8856 Google Scholar
L. GradyE. L. Schwartz,
“Isoperimetric graph partitioning for image segmentation,”
IEEE Trans. Pattern Anal. Mach. Intel., 28
(3), 469
–475
(2006). http://dx.doi.org/10.1109/TPAMI.2006.57 ITPIDJ 0162-8828 Google Scholar
L. Grady,
“Random walks for image segmentation,”
IEEE Trans. Pattern Anal. Mach. Intel., 28
(11), 1768
–1783
(2006). http://dx.doi.org/10.1109/TPAMI.2006.233 ITPIDJ 0162-8828 Google Scholar
W. Yanget al.,
“User-friendly interactive image segmentation through unified combinatorial user inputs,”
IEEE Trans. Image Proc., 19
(9), 2470
–2479
(2010). http://dx.doi.org/10.1109/TIP.2010.2048611 IIPRE4 1057-7149 Google Scholar
S. Xianget al.,
“Interactive image segmentation with multiple linear reconstructions in Windows,”
IEEE Trans. Multimedia, 13
(2), 342
–352
(2011). http://dx.doi.org/10.1109/TMM.2010.2103930 ITMUF8 1520-9210 Google Scholar
G. Liuet al.,
“Unsupervised object segmentation with a hybrid graph model (HGM),”
IEEE Trans. Pattern Anal. Mach. Intel., 32
(5), 910
–924
(2010). http://dx.doi.org/10.1109/TPAMI.2009.40 ITPIDJ 0162-8828 Google Scholar
L. DingA. Yilmaz,
“Interactive image segmentation using probabilistic hypergraphs,”
Elsevier Pattern Recogn., 43
(5), 1863
–1873
(2010). http://dx.doi.org/10.1016/j.patcog.2009.11.025 PTNRA8 0031-3203 Google Scholar
W. Taoet al.,
“Interactively multiphase image segmentation based on variational formulation and graph cuts,”
Elsevier Pattern Recogn., 43
(10), 3208
–3218
(2010). http://dx.doi.org/10.1016/j.patcog.2010.04.014 PTNRA8 0031-3203 Google Scholar
M. B. SalahA. MiticheI. B. Ayed,
“Multiregion image segmentation by parametric kernel graph cuts,”
IEEE Trans. Image Proc., 20
(2), 545
–557
(2011). http://dx.doi.org/10.1109/TIP.2010.2066982 IIPRE4 1057-7149 Google Scholar
S. MakrogiannisG. EconomouS. Fotopoulos,
“A region dissimilarity relation that combines feature-space and spatial information for color image segmentation,”
IEEE Trans. Sys. Man Cyber.B Cyber., 35
(1), 44
–53
(2005). http://dx.doi.org/10.1109/TSMCB.2004.837756 ITSCFI 1083-4419 Google Scholar
S. Makrogianniset al.,
“Segmentation of color images using multiscale clustering and graph theoretic region synthesis,”
IEEE Trans. Sys. Man Cyber. A Sys. Humans, 35
(2), 224
–238
(2005). http://dx.doi.org/10.1109/TSMCA.2004.832820 ITSHFX 1083-4427 Google Scholar
B. SumengenB. S. Manjunath,
“Graph partitioning active contours (GPAC) for image segmentation,”
IEEE Trans. Pattern Anal. Mach. Intel., 28
(4), 509
–521
(2006). http://dx.doi.org/10.1109/TPAMI.2006.76 ITPIDJ 0162-8828 Google Scholar
A. V. Wangenheimet al.,
“Color image segmentation guided by a color gradient network,”
Elsevier Pattern Recogn. Lett., 28
(13), 1795
–1803
(2007). http://dx.doi.org/10.1016/j.patrec.2007.05.009 PRLEDG 0167-8655 Google Scholar
A. V. Wangenheimet al.,
“Color image segmentation using an enhanced gradient network method,”
Elsevier Pattern Recogn. Lett., 30
(15), 1404
–1412
(2009). http://dx.doi.org/10.1016/j.patrec.2009.07.005 PRLEDG 0167-8655 Google Scholar
M. P. KumarP. H. S. TorrA. Zisserman,
“OBJCUT: efficient segmentation using top-down and bottom-up cues,”
IEEE Trans. Pattern Anal. Mach. Intel., 32
(3), 530
–545
(2010). http://dx.doi.org/10.1109/TPAMI.2009.16 ITPIDJ 0162-8828 Google Scholar
C. Couprieet al.,
“Power watershed: a unifying graph-based optimization framework,”
IEEE Trans. Pattern Anal. Mach. Intel., 33
(7), 1384
–1399
(2011). http://dx.doi.org/10.1109/TPAMI.2010.200 ITPIDJ 0162-8828 Google Scholar
R. C. GonzalezR. E. Woods, Digital Image Processing, 3rd ed.Pearson/Prentice Hall Ltd., Upper Saddle River, New Jersey
(2008). Google Scholar
H. GaoW. C. SiuC. H. Hou,
“Improved techniques for automatic image segmentation,”
IEEE Trans. Circuits Sys. Video Tech., 11
(12), 1273
–1280
(2001). http://dx.doi.org/10.1109/76.974681 ITCTEM 1051-8215 Google Scholar
H. Gaoet al.,
“Marker-based image segmentation relying on disjoint set union,”
Elsevier Signal Proc. Image Comm., 21
(2), 100
–112
(2006). http://dx.doi.org/10.1016/j.image.2005.06.008 SPICEF 0923-5965 Google Scholar
P. R. HillC. N. CanagarajahD. R. Bull,
“Image segmentation using a texture gradient based watershed transform,”
IEEE Trans. Image Proc., 12
(12), 1618
–1633
(2003). http://dx.doi.org/10.1109/TIP.2003.819311 IIPRE4 1057-7149 Google Scholar
H. T. NguyenM. WorringR. Boomgaard,
“Watersnakes: energy-driven watershed segmentation,”
IEEE Trans. Pattern Anal. Mach. Intel., 25
(3), 330
–342
(2003). http://dx.doi.org/10.1109/TPAMI.2003.1182096 ITPIDJ 0162-8828 Google Scholar
I. VanhamelI. PratikakisH. Sahli,
“Multiscale gradient watersheds of color images,”
IEEE Trans. Image Proc., 12
(6), 617
–626
(2003). http://dx.doi.org/10.1109/TIP.2003.811490 IIPRE4 1057-7149 Google Scholar
J. B. KimH. J. Kim,
“Multiresolution-based watersheds for efficient image segmentation,”
Elsevier Pattern Recogn. Lett., 24
(1–3), 473
–488
(2003). http://dx.doi.org/10.1016/S0167-8655(02)00270-2 PRLEDG 0167-8655 Google Scholar
C. R. Jung,
“Unsupervised multiscale segmentation of color images,”
Elsevier Pattern Recogn. Lett., 28
(4), 523
–533
(2007). http://dx.doi.org/10.1016/j.patrec.2006.10.001 PRLEDG 0167-8655 Google Scholar
P. Arbeláezet al.,
“Contour detection and hierarchical image segmentation,”
IEEE Trans. Pattern Anal. Mach. Intel., 33
(5), 898
–916
(2011). http://dx.doi.org/10.1109/TPAMI.2010.161 ITPIDJ 0162-8828 Google Scholar
R. J. O’CallaghanD. R. Bull,
“Combined morphological-spectral unsupervised image segmentation,”
IEEE Trans. Image Proc., 14
(1), 49
–62
(2005). http://dx.doi.org/10.1109/TIP.2004.838695 IIPRE4 1057-7149 Google Scholar
S. Makrogianniset al.,
“Watershed-based multiscale segmentation method for color images using automated scale selection,”
J. Elec. Imag., 14
(3), 033007
(2005). http://dx.doi.org/10.1117/1.1995711 JEIME5 1017-9909 Google Scholar
H. D. ChengJ. Li,
“Fuzzy homogeneity and scale-space approach to color image segmentation,”
Elsevier Pattern Recogn., 36
(7), 1545
–1562
(2003). http://dx.doi.org/10.1016/S0031-3203(02)00293-5 PTNRA8 0031-3203 Google Scholar
S. B. Chaabaneet al.,
“Colour image segmentation using homogeneity method and data fusion techniques,”
EURASIP J. Adv. Signal Proc., 2010
(367297), 1
–11
(2010). http://dx.doi.org/10.1155/2010/367297 Google Scholar
S. K. ChoyM. L. TangC. S. Tong,
“Image segmentation using fuzzy region competition and spatial/frequency information,”
IEEE Trans. Image Proc., 20
(6), 1473
–1484
(2011). http://dx.doi.org/10.1109/TIP.2010.2095023 IIPRE4 1057-7149 Google Scholar
A. ProtiereG. Sapiro,
“Interactive image segmentation via adaptive weighted distances,”
IEEE Trans. Image Proc., 16
(4), 1046
–1057
(2007). http://dx.doi.org/10.1109/TIP.2007.891796 IIPRE4 1057-7149 Google Scholar
S. Xianget al.,
“Interactive natural image segmentation via spline regression,”
IEEE Trans. Image Proc., 18
(7), 1623
–1632
(2009). http://dx.doi.org/10.1109/TIP.2009.2018570 IIPRE4 1057-7149 Google Scholar
X. BaiG. Sapiro,
“Geodesic matting: a framework for fast interactive image and video segmentation and matting,”
Inter. J. Comp. Vis., 82
(2), 113
–132
(2009). http://dx.doi.org/10.1007/s11263-008-0191-z IJCVEQ 0920-5691 Google Scholar
H. LiC. Shen,
“Interactive color image segmentation with linear programming,”
Mach. Vis. App., 21
(4), 403
–412
(2010). http://dx.doi.org/10.1007/s00138-008-0171-x MVAPEO 0932-8092 Google Scholar
L. ShiB. Funt,
“Quaternion color texture segmentation,”
Elsevier Comp. Vis. Image Understanding, 107
(1–2), 88
–96
(2007). http://dx.doi.org/10.1016/j.cviu.2006.11.014 CVIUF4 1077-3142 Google Scholar
Ö. N. SubakanB. C. Vemuri,
“A quaternion framework for color image smoothing and segmentation,”
Inter. J. Comp. Vis., 91
(3), 233
–250
(2011). http://dx.doi.org/10.1007/s11263-010-0388-9 IJCVEQ 0920-5691 Google Scholar
J. Shottonet al.,
“TextonBoost: Joint appearance, shape and context modeling for multi-class object recognition and segmentation,”
in European Conf. Comp. Vis. (ECCV),
1
–15
(2006). Google Scholar
J. ShottonM. JohnsonR. Cipolla,
“Semantic texton forests for image categorization and segmentation,”
in IEEE Inter. Conf. Comp. Vis. Pattern Recogn. (CVPR),
1
–8
(2008). Google Scholar
J. Shottonet al.,
“TextonBoost for image understanding: multi-class object recognition and segmentation by jointly modeling texture, layout, and context,”
Inter. J. Comp. Vis., 81
(1), 2
–23
(2009). http://dx.doi.org/10.1007/s11263-007-0109-1 IJCVEQ 0920-5691 Google Scholar
Z. Yuet al.,
“Bag of textons for image segmentation via soft clustering and convex shift,”
in IEEE Inter. Conf. Comp. Vis. Pattern Recogn. (CVPR),
(2012). Google Scholar
C. WangL. Guan,
“Graph cut video object segmentation using histogram of oriented gradients,”
in IEEE Inter. Symposium on Circuits and Systems (ISCAS),
2590
–2593
(2008). Google Scholar
P. NammalwarO. GhitaP. Whelan,
“A generic framework for colour texture segmentation,”
Sensor Review, 30
(1), 69
–79
(2010). http://dx.doi.org/10.1108/02602281011010817 SNRVDY 0260-2288 Google Scholar
X. Liet al.,
“Graph cuts based image segmentation using local color and texture,”
in 4th IEEE Inter. Congress on Image and Signal Proc. (CISP),
1251
–1255
(2011). Google Scholar
C. RohkohlK. Engel,
“Efficient image segmentation using pairwise pixel similarities,”
in 29th Annual Symposium of the German Association for Pattern Recogn.,
254
–263
(2007). Google Scholar
A. Levinshteinet al.,
“TurboPixels: fast superpixels using geometric flows,”
IEEE Trans. Pattern Anal. Mach. Intel., 31
(12), 2290
–2297
(2009). http://dx.doi.org/10.1109/TPAMI.2009.96 ITPIDJ 0162-8828 Google Scholar
R. Achantaet al.,
“SLIC superpixels compared to state-of-the-art superpixel methods,”
IEEE Trans. Pattern Anal. Mach. Intell., 34
(11), 2274
–2282
(2012). Google Scholar
M. Liuet al.,
“Entropy rate superpixel segmentation,”
in IEEE Inter. Conf. Comp. Vis. Pattern Recogn. (CVPR),
2097
–2104
(2011). Google Scholar
Y. Artan,
“Interactive image segmentation using machine learning techniques,”
in IEEE Canadian Conf. Comp. Robot Vis. (CRV),
264
–269
(2011). Google Scholar
Z. LiX. WuS. Chang,
“Segmentation using superpixels: a bipartite graph partitioning approach,”
in IEEE Inter. Conf. Comp. Vis. Pattern Recogn. (CVPR),
(2012). Google Scholar
M. A. HoangJ. M. GeusebroekA. W. M. Smeulders,
“Color texture measurement and segmentation,”
Elsevier Sig. Proc., 85
(2), 265
–275
(2005). http://dx.doi.org/10.1016/j.sigpro.2004.10.009 SPRODR 0165-1684 Google Scholar
E. Vazquezet al.,
“Describing reflectances for color segmentation robust to shadows, highlights, and textures,”
IEEE Trans. Pattern Anal. Mach. Intel., 33
(5), 917
–930
(2011). http://dx.doi.org/10.1109/TPAMI.2010.146 ITPIDJ 0162-8828 Google Scholar
X. Y. WangT. WangJ. Bu,
“Color image segmentation using pixel wise support vector machine classification,”
Elsevier Pattern Recogn., 44
(4), 777
–787
(2011). http://dx.doi.org/10.1016/j.patcog.2010.08.008 PTNRA8 0031-3203 Google Scholar
Z. YuH. S. WongG. Wen,
“A modified support vector machine and its application to image segmentation,”
Elsevier Image Vis. Comp., 29
(1), 29
–40
(2011). http://dx.doi.org/10.1016/j.imavis.2010.08.003 IVCODK 0262-8856 Google Scholar
L. MacaireN. VandenbrouckeJ. G. Postaire,
“Color image segmentation by analysis of subset connectedness and color homogeneity properties,”
Elsevier Comp. Vis. Image Understanding, 102
(1), 105
–116
(2006). http://dx.doi.org/10.1016/j.cviu.2005.12.001 CVIUF4 1077-3142 Google Scholar
T. ZöllerJ. M. Buhmann,
“Robust image segmentation using resampling and shape constraints,”
IEEE Trans. Pattern Anal. Mach. Intel., 29
(7), 1147
–1164
(2007). http://dx.doi.org/10.1109/TPAMI.2007.1150 ITPIDJ 0162-8828 Google Scholar
E. BorensteinS. Ullman,
“Combined top-down/bottom-up segmentation,”
IEEE Trans. Pattern Anal. Mach. Intel., 30
(12), 2109
–2125
(2008). http://dx.doi.org/10.1109/TPAMI.2007.70840 ITPIDJ 0162-8828 Google Scholar
G. DelyonF. GallandP. Réfrégier,
“Minimal stochastic complexity image partitioning with unknown noise model,”
IEEE Trans. Image Proc., 15
(10), 3207
–3212
(2006). http://dx.doi.org/10.1109/TIP.2006.877484 IIPRE4 1057-7149 Google Scholar
A. Barderaet al.,
“Image segmentation using information bottleneck method,”
IEEE Trans. Image Proc., 18
(7), 1601
–1612
(2009). http://dx.doi.org/10.1109/TIP.2009.2017823 IIPRE4 1057-7149 Google Scholar
Y. Z. Songet al.,
“In search of perceptually salient groupings,”
IEEE Trans. Image Proc., 20
(4), 935
–947
(2011). http://dx.doi.org/10.1109/TIP.2010.2087766 IIPRE4 1057-7149 Google Scholar
A. M. UsóF. PlaP. G. Sevilla,
“Unsupervised colour image segmentation by low-level perceptual grouping,”
Pattern Anal. App., 1
–14
(2011). Google Scholar
S. GhoshJ. Pfeiffer IIIJ. Mulligan,
“A general framework for reconciling multiple weak segmentations of an image,”
in IEEE Workshop on App. Comp. Vis. (WACV),
1
–8
(2009). Google Scholar
S. VitaladevuniR. Basri,
“Co-clustering of image segments using convex optimization applied to EM neuronal reconstruction,”
in IEEE Inter. Conf. Comp. Vis. Pattern Recog. (CVPR),
2203
–2210
(2010). Google Scholar
D. GlasnerS. VitaladevuniR. Basri,
“Contour-based joint clustering of multiple segmentations,”
in IEEE Inter. Conf. Comp. Vis. Pattern Recogn. (CVPR),
2385
–2392
(2011). Google Scholar
C. Rotheret al.,
“Cosegmentation of image pairs by histogram matching—incorporating a global constraint into MRFs,”
in IEEE Inter. Conf. Comp. Vis. Pattern Recogn. (CVPR),
993
–1000
(2006). Google Scholar
D. ChengM. Figueiredo,
“Cosegmentation for image sequences,”
in 14th IEEE Inter. Conf. on Image Anal. Proc. (ICIAP),
635
–640
(2007). Google Scholar
D. HochbaumV. Singh,
“An efficient algorithm for co-segmentation,”
in IEEE Inter. Conf. Comp. Vis. Pattern Recogn. (CVPR),
269
–276
(2009). Google Scholar
L. MukherjeeV. SinghC. Dyer,
“Half-integrality based algorithms for cosegmentation of images,”
in IEEE Inter. Conf. Comp. Vis. Pattern Recogn. (CVPR),
2028
–2035
(2009). Google Scholar
D. BatraA. KowdleD. Parikh,
“iCoseg: interactive cosegmentation with intelligent scribble guidance,”
in IEEE Inter. Conf. Comp. Vis. Pattern Recogn. (CVPR),
3169
–3176
(2010). Google Scholar
K. ChangT. LiuS. Lai,
“From co-saliency to co-segmentation: an efficient and fully unsupervised energy minimization model,”
in IEEE Inter. Conf. Comp. Vis. Pattern Recogn. (CVPR),
2129
–2136
(2011). Google Scholar
S. VicenteC. RotherV. Kolmogorov,
“Object cosegmentation,”
in IEEE Inter. Conf. Comp. Vis. Pattern Recogn. (CVPR),
2217
–2224
(2011). Google Scholar
A. JoulinF. BachJ. Ponce,
“Multi-class cosegmentation,”
in IEEE Inter. Conf. Comp. Vis. Pattern Recog. (CVPR),
542
–549
(2012). Google Scholar
G. KimE. Xing,
“On multiple foreground cosegmentation,”
in IEEE Inter. Conf. Comp. Vis. Pattern Recogn. (CVPR),
837
–844
(2012). Google Scholar
Y. J. Zhang,
“A survey on evaluation methods for image segmentation,”
Elsevier Pattern Recogn., 29
(8), 1335
–1346
(1996). http://dx.doi.org/10.1016/0031-3203(95)00169-7 PTNRA8 0031-3203 Google Scholar
R. UnnikrishnanC. PantofaruM. Hebert,
“Toward objective evaluation of image segmentation algorithms,”
IEEE Trans. Pattern Anal. Mach. Intel., 29
(6), 929
–944
(2007). http://dx.doi.org/10.1109/TPAMI.2007.1046 ITPIDJ 0162-8828 Google Scholar
R. UnnikrishnanM. Hebert,
“Measures of similarity,”
in IEEE Workshop on App. Comp. Vis.,
394
–400
(2005). Google Scholar
Biography Sreenath Rao Vantaram received his BTech (equivalent BS) degree in electronics and communication engineering from the Jawaharlal Nehru Technological University (JNTU), Andhra Pradesh, India, in 2006 and his MS in electrical engineering with focus area in signal, image, and video processing, from the Rochester Institute of Technology (RIT), Rochester, NY, in 2009. He is currently pursuing his PhD degree in imaging science at the Chester F. Carlson Center for Imaging Science, at RIT, focused on developing algorithms that facilitate 2- and 3-D segmentation of multimodal imagery. His research interests are in the areas of computer vision, digital image/video processing, understanding, and analysis including segmentation, classification, object recognition, tracking, etc. to name a few.  Eli Saber is a professor in the electrical engineering department at the Rochester Institute of Technology. Prior to that, he worked for Xerox Corporation from 1988 until 2004 in a variety of positions ending as product development scientist and manager. He received the BS degree in electrical and computer engineering from the University of Buffalo in 1988, and the MS and PhD degrees in the same discipline from the University of Rochester in 1992 and 1996 respectively. His research interests are in the areas of image/video processing, computer vision and biomedical imaging. He is a senior member of IEEE and IS&T, a member of the Image, Video, and Multidimensional Signal Processing Technical Committee and member/former chair of IEEE Industry Technology Committee. He is an area editor for the Journal of Electronic Imaging. He has served on several conference committees including Finance chair for ICIP 2002, Tutorial Chair for ICIP 2007 and ICIP 2009 and General Chair for ICIP 2012. He holds many conference and journal publications. |