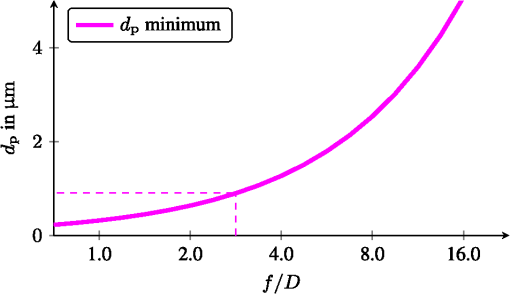
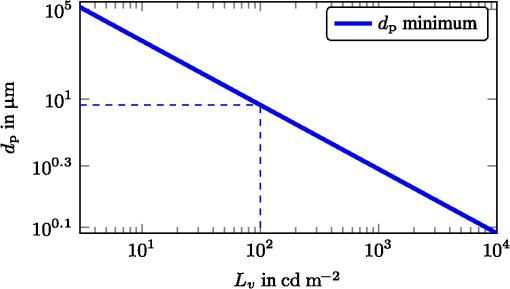
1.

Introduction

The steady progress in semiconductor technology allows the manufacturing of smaller and smaller structures and image sensors with ever shrinking pixel sizes. One can get the impression that the pixel size is just limited by the technology and even smaller pixels are desirable. Today, consumer products with pixel sizes $d_{\text{p}}=1.4\mathrm{\mu m}$ are already on the market and devices with $d_{\text{p}}=1.1\mathrm{\mu m}$ are in production.¹ In comparison, photo receptors in the human eye are reported to be larger than 3 μm.²

The general modeling of light is well understood,³ and simulation with commercial tools like ISET⁴ is possible. In contrast, this letter addresses parameters like aperture and pixel size and their photometric consequences for modeling the amount of light that is available in a digital video camera system. One of the design parameters is the resulting image quality. With small pixels only a few photons will hit a single pixel during an exposure period and the signal-to-noise power ratio (SNR) will be poor due to shot noise.⁵ Apart from all technological limitations, this physical boundary limits the performance of today’s video cameras.

2.

Image Acquisition Model

The scene radiates a certain amount of light. This is described by an average radiance in object space $L_{\text{obj}}$. The sensor sees an effective amount of light equivalent to the cone with a solid angle $\mathrm{\Omega }$ as shown in Fig. 1(a). This cone is defined by the sphere of radius equal to the focal length $f$ and a circular aperture disk with diameter $D$. The solid angle thus calculates to⁶

Fig. 1

Parameters of (a) focal length $f$, aperture diameter $D$ and resulting solid angle $\mathrm{\Omega }$ and (b) quadratic pixels with fill factor 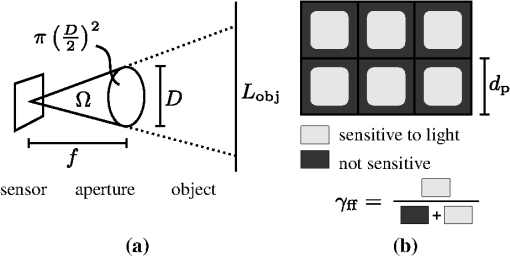${\gamma }_{\mathrm{ff}}$.

On the sensor some area is used for interconnects and transistors so that only some of the area is sensitive to light. Figure 1(b) shows pixels of size $d_{\text{p}}$. The ratio of active to total areas is expressed as an effective sensor fill factor ${\gamma }_{\mathrm{ff}}$. Even with clever manufacturing like micro-lenses or back side illumination, ${\gamma }_{\mathrm{ff}}<1$ holds. A single pixel thus captures a certain amount of radiant power (radiant flux) ${\mathrm{\Phi }}_{\text{pix}}$ of the sensor irradiance

SNR is a parameter that is directly visible in the final images. For answering the original question, we can combine the above equations. This leads to

3.

Results for Ideal System

At first we assume ideal technology. A typical indoor scene is illuminated with a luminance of $L_v=100\mathrm{cd}{\mathrm{m}}^{-2}$.⁹ For the peak sensitivity of the human eye at a wavelength of $\lambda =555\mathrm{nm}$ the SI unit candela is defined¹⁰ as radiant intensity of $1/683\mathrm{W}{\mathrm{sr}}^{-1}$. The radiance in object space is then

The influence of different apertures is shown in Fig. 2. With larger aperture diameters, even smaller pixels can be used. A variation of luminance is also possible: In practice, the human color perception (photoptic vision) starts at $L_v=3\mathrm{cd}{\mathrm{m}}^{-2}$.⁹ The luminance in daylight exterior scenarios is typically $L_v={10}^4\mathrm{cd}{\mathrm{m}}^{-2}$.⁹ The resulting minimum pixel sizes thus range from 5 to 0.09 μm as shown in Fig. 3.

Fig. 2

Minimum pixel sizes for photon limited system with varying apertures, ideal system with $\mathrm{SNR}=\sqrt{1000}$ and scene with luminance of $L_v=100\mathrm{cd}{\mathrm{m}}^{-2}$, dashed line for $f/D=2.8$.

Fig. 3

Minimum pixel sizes for photon limited system with varying luminance, ideal system with $\mathrm{SNR}=\sqrt{1000}$ and aperture $f/D=2.8$, dashed line for $L_v=100\mathrm{cd}{\mathrm{m}}^{-2}$.

4.

Radiometric Modeling

Up to now, we used monochromatic light only. We now extend this and also include the spectral distribution of light. Again, we start with a scene with a luminance of $L_v=100\mathrm{cd}{\mathrm{m}}^{-2}$. Now, the light is made up of radiation from a light bulb. This is modeled as a black body at a certain color temperature $T$ and a spectral radiance of

Fig. 4

Spectral radiance of black bodies with temperatures $T$, intensity scaled to be perceived as luminance of 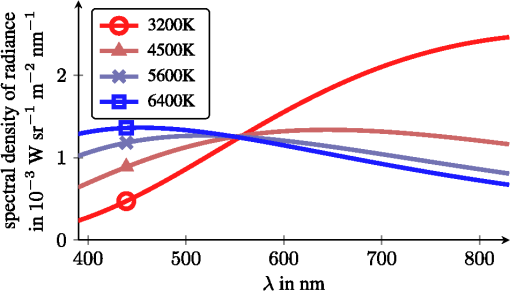$100\mathrm{cd}{\mathrm{m}}^{-2}$.

Today, most cameras are used to capture scenes for later viewing by a human. The camera should therefore create a representation of the scene that is similar to that of the human visual system. We simulate an ideal camera with the spectral sensitivity curves based on the Stockman and Sharpe cone measurements of the human eye.¹² The corresponding spectral sensitivity functions for long (L), medium (M) and short (S) wavelengths are shown in Fig. 5. However, we assume an ideal camera with ideal color filters and material without any attenuation (${\eta }_{\mathrm{qe}}=1$) at peak efficiency.

Fig. 5

Sensitivity functions of 10-deg cone fundamentals for $L$, $M$ and $S$ cone and luminous efficiency function 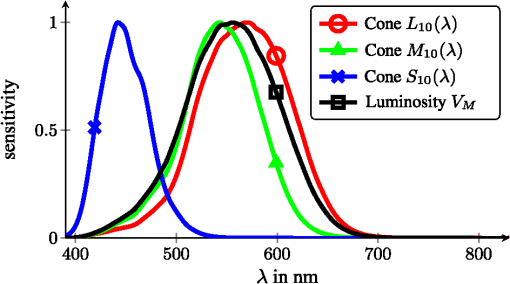$V_m$.

In Table 1, the resulting minimum pixel sizes are shown for the radiometric simulation. The luminosity case with monochromatic light at $\lambda =555\mathrm{nm}$ corresponds to the ideal simulation from above. There is less than 10% error for the simulation with $L$ and $M$ cones compared to the luminosity. This is plausible from the high similarity of the respective sensitivity curves. However, the capturing of blue light (short wavelengths with cone $S$) requires larger pixels. At short wavelengths, the individual photons have a higher energy and thus, there are fewer for a given radiant flux. This explains the problem of inferior performance of blue color channels in typical digital cameras. The extreme case of observing monochromatic green light with a short wavelength sensitivity leads to even fewer photons and would require pixels with 26 μm. In general, the monochromatic calculation is only slightly optimistic but gives a good approximation to a radiometric computation.

Table 1

Minimum pixel sizes (in μm) based on radiometric calculations for light sources with black body radiation of temperature T and monochromatic light source.

5.

Results with Current Technology

The above numbers represent the theoretical limit for ideal sensors. In practice, a real world camera does not achieve these numbers. For example, a highly optimized three layer stacked image sensor is reported by Hannebauer et al.¹³ For pixels of size $d_{\text{p}}=4.8\mathrm{\mu m}$ a high fill factor of ${\gamma }_{\mathrm{ff}}=0.95$ and quantum efficiency of ${\eta }_{\mathrm{qe}}=0.8$ is possible with many (costly) optimizations. In current 1.4 μm consumer grade sensors the backside illumination (BSI) technology enables close to 100% fill factor.¹⁴ For color imaging, the spectral sensitivity is not without attenuation and peak quantum efficiencies of about ${\eta }_{\mathrm{qe}}\approx 0.5$ are reported by OmniVision¹⁴ and Aptina.¹⁵ In scientific CMOS sensors, the combined sensor readout noise is reported as low as $1.3\text{electrons}/\text{pixel}$¹⁶ and can thus be neglected among 1000 electrons. The combined assumption of ${\eta }_{\text{lens}}=0.95$, ${\gamma }_{\mathrm{ff}}=0.95$ and ${\eta }_{\mathrm{qe}}=0.5$ leads to a minimum pixel size of $d_{\text{p},\min }=1.34\mathrm{\mu m}$. With mass-market sensors and additional noise,⁸ larger pixels are required.

These small pixels also reach another technological limit of decreasing full well capacity. For example Aptina reports¹⁵ $C=5000$ electrons, which leaves only a dynamic range of $5:1$ from noise visibility⁵ to overexposure. As a result, most of the image will still look noisy. However, this is a technological challenge that could be addressed with multiple readouts during the exposure.¹⁷

Another limitation comes with optical diffraction. Even in ideal optics the achievable resolution of a camera system is limited. The Sparrow criterion suggests³ that there is no gain in resolution below a critical pixel size of $d_{\text{p},\text{crit}}=\frac{\lambda }{2}·f/D$. For our example of $f/D=2.8$ and $\lambda =555\mathrm{nm}$, we obtain $d_{\text{p},\text{crit}}=0.78\mathrm{\mu m}$. Achieving this limit, however, is challenging, especially in the off-axis field, and leads to expensive optics. A further decrease in aperture requires a dramatic increase of the technological efforts and smaller tolerances for optics manufacturers.

6.

Conclusion

In our photometric analysis, we discuss the number of photons per pixel. With small pixels the image quality is limited by shot noise, and for indoor scenarios the current video cameras are surprisingly close to this fundamental limit. We estimate that even with ideal technology, a pixel size below $d_{\text{p}}=0.9\mathrm{\mu m}$ will not capture enough light to generate visually pleasing videos any more. Current technology is far from perfect and with optimistic assumptions, the limit at $d_{\text{p}}=1.34\mathrm{\mu m}$ is close to current sensors. However, for other imaging scenarios like outdoor daylight still photography, there is plenty of room at the bottom.