|
|
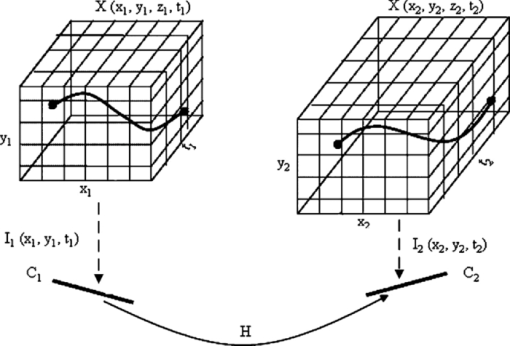
1.IntroductionTemporal alignment of video sequences is important in applications such as superresolution imaging,1 robust multiview surveillance,2 and mosaicking. In some applications, it is required to align video sequences from two similar scenes, where analogous motions have different trajectories through the video sequence. Figure 1 illustrates two similar motions occurring in related 3-D planar scenes with respect to time. Camera 1 views 3-D scene [TeX:] $X(X_1 ,Y_1 ,Z_1 ,t_1 )$ in view 1(ν1) and acquires video [TeX:] $I_1 (x_1 ,y_1 ,t_1 )$. Camera 2 views another 3-D scene[TeX:] $X(X_2 ,Y_2 ,Z_{2,} \,t_1 )$in view 2 (ν2) and acquires video [TeX:] $I_2 (x_2 ,y_2 ,t_2 )$. Note that the motions in these two scenes are similar but have dynamic time shift. The homography matrix H is typically used to represent the spatial relationship between these two views. A typical schematic for temporal alignment is shown in Fig. 2. Note that for the sake of correlating two videos and representing the motions, features are extracted and tracked separately in each video. Robust view-invariance tracker methods are used to generate feature trajectories [TeX:] ${\cal F}_1 (x_1 ,y_1 ,t_1 )$ and [TeX:] ${\cal F}_2 (x_2 ,y_2 ,t_2 )$ from video [TeX:] $I_1$ and [TeX:] $I_2$, respectively. Existing techniques vary on how to compute the temporal alignments. Giese and Poggio3 computed the temporal alignment of activities of different people using dynamic time warping (DTW) between the feature trajectories, but limited their technique to a fixed viewpoint. Rao 4 used a rank-constraint-based technique (RCB) in DTW to calculate the synchronization. Such techniques only consider unidirectional alignment,3, 4 i.e., they project the trajectory from one scene to the other, which designates one view as the reference for computing the temporal alignment. Such techniques introduce the bias toward the reference trajectory, i.e., due to the noise and imperfection of the obtained reference trajectory, such a technique will produce erroneous alignment. Therefore, for the sake of minimizing the bias, one should consider computing the alignment in a symmetric way. Singh 5 formulated a symmetric transfer error (STE) as a functional of regularized temporal warp. The technique determines the time warp that has the smallest STE. It then chooses one of the symmetric warps as the final temporal alignment. The STE technique provides better results than unidirectional alignment schemes. The accuracy of the temporal alignment can be improved further, since the STE technique does not really eliminate the reference-view bias between two sequences. In this work, we propose an unbiased bidirectional dynamic time warping (UBDTW) technique that can remove biasing and provide more accurate results. 2.Proposed TechniqueThe schematic of the proposed temporal alignment technique is shown in Fig. 3. The technique consists of three steps which are explained in the following sections. 2.1.Bidirectional ProjectionsSince feature trajectories represent the activities in the video sequences, we compute the projections of the feature trajectories [TeX:] ${\cal F}_1$ from scene 1 to 2 and [TeX:] ${\cal F}_2$ from scene 2 to 1 using Eq. 1 as follows: [TeX:] \documentclass[12pt]{minimal}\begin{document}\begin{equation*}
{\cal F}^p _2 (x^\prime _1 ,y'_1 ,t_1 ) = H_{1 \to 2} \,\cdot\,{\cal F}_1 (x_1 ,y_1 ,t_1 ),
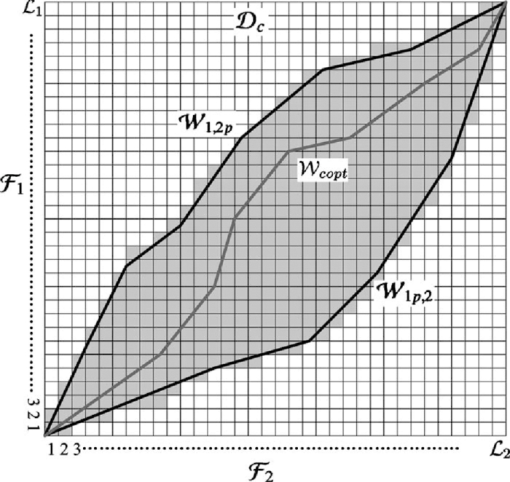
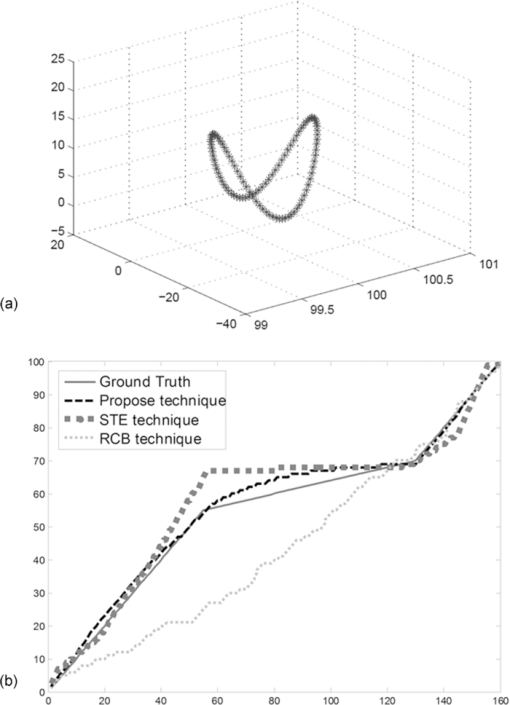
\end{equation*}\end{document} Eq. 1[TeX:] \documentclass[12pt]{minimal}\begin{document}\begin{equation} {\cal F}^p _1 (x^\prime _2 ,y'_2 ,t_2 ) = H_{2 \to 1} \,\cdot\,{\cal F}_2 (x_2 ,y_2 ,t_2 ), \end{equation}\end{document}2.2.Computation of Symmetric WarpsOnce we obtain two pairs of feature trajectories, [TeX:] $({\cal F}_1 ,{\cal F}_2 ^p )$ and [TeX:] $({\cal F}_1 ^p ,{\cal F}_2 )$, we compute the symmetric warps [TeX:] ${\cal W}_{1,2p}$ and [TeX:] ${\cal W}_{1p,2}$ using regularized DTW. We construct the warp [TeX:] ${\cal W}$ as follows: Eq. 2[TeX:] \documentclass[12pt]{minimal}\begin{document}\begin{equation} {\cal W} = w_1 ,w_2 ,\ldots,w_{L\,} \,\,\max ({\cal L}_1 ,{\cal L}_2 ) \le L < {\cal L}_1 + {\cal L}_2 , \end{equation}\end{document}Eq. 3[TeX:] \documentclass[12pt]{minimal}\begin{document}\begin{equation} {\rm dist}({\cal W}) = \sum\limits_{k = 1}^L {{\rm dist}[{\cal F}(i_k ),{\cal F}^p (j_k )],} \end{equation}\end{document}Eq. 4[TeX:] \documentclass[12pt]{minimal}\begin{document}\begin{equation} {\rm dist}[{\cal F}(i),{\cal F}^p (j)] = ||{\cal F}(i) - {\cal F}^p (j)||^2 + w\,\,{\rm reg}, \end{equation}\end{document}Eq. 5[TeX:] \documentclass[12pt]{minimal}\begin{document}\begin{equation} {\rm reg} = ||\partial {\cal F}(i) - \partial {\cal F}^p (j)||^2 + ||\partial ^2 {\cal F}(i) - \partial ^2 {\cal F}^p (j)||^2 , \end{equation}\end{document}To find the optimal warp, an accumulated distance matrix is created. The value of the element in the accumulated distance matrix is: Eq. 6[TeX:] \documentclass[12pt]{minimal}\begin{document}\begin{equation} {\bm {\cal D}}(i,j) = {\rm dist}[{\cal F}(i),{\cal F}^p (j)] + \min (\phi ), \end{equation}\end{document}Eq. 7[TeX:] \documentclass[12pt]{minimal}\begin{document}\begin{equation} \phi = [{\bm {\cal D}}(i - 1,j),{\bm {\cal D}}(i - 1, \,j - 1),{\bm {\cal D}}(i,j - 1)]. \end{equation}\end{document}2.3.Optimal Warp CalculationNote that we calculated symmetric warps [TeX:] ${\cal W}_{1,2p}$ and [TeX:] ${\cal W}_{1p,2}$, and corresponding distance matrixes [TeX:] ${\bm {\cal D}}_{1,2p}$ and [TeX:] ${\bm {\cal D}}_{1p,2}$ in the last step. However, the warps still have bias ([TeX:] ${\cal W}_{1,2p}$ biased toward [TeX:] ${\cal F}_1$ while [TeX:] ${\cal W}_{1p,2}$ is biased toward [TeX:] ${\cal F}_2$). To minimize the effect of biasing on alignment, we first combine [TeX:] ${\bm {\cal D}}_{1,2p}$ and [TeX:] ${\bm {\cal D}}_{1p,2}$ to make a new distance matrix [TeX:] ${\bm {\cal D}}_c$ as follows: Eq. 8[TeX:] \documentclass[12pt]{minimal}\begin{document}\begin{equation} {\bm {\cal D}}_c = {\bm {\cal D}}_{1,2p} + {\bm {\cal D}}_{1p,2} . \end{equation}\end{document}Eq. 9[TeX:] \documentclass[12pt]{minimal}\begin{document}\begin{equation} \min ({\cal W}_{1,2} ,{\cal W}_{2,1} ) \le {\cal W}_c \le \max ({\cal W}_{1,2} ,{\cal W}_{2,1} ). \end{equation}\end{document}Eq. 10[TeX:] \documentclass[12pt]{minimal}\begin{document}\begin{equation} {\cal W}_{\rm copt} = \arg _{{\cal W}_c } \min [{\rm dist}({\cal W}_c )]. \end{equation}\end{document}3.Experiments and Comparative AnalysisWe evaluated our technique using both synthetic and real videos and compared it with RCB4 and STE techniques.5 3.1.Synthetic Data EvaluationIn the synthetic data evaluation, we generate planar trajectories 100 frames long using a pseudorandom number gen- erator. These trajectories are then projected onto two image planes using user-defined camera projection matrices. A 60-frames-long time warp is then applied to a section of one of the trajectory projections. The temporal alignment techniques are then applied to the synthetic trajectories. The test was repeated on 100 different synthetic trajectories and 100 similar trajectories with noise added. The added noise was a normally distributed random variate, with zero mean and variance [TeX:] $\sigma ^2 = 0.1$. The mean absolute error between the warp obtained by different techniques and the ground truth is computed as the evaluation metric. The results are shown in Table 1. The percentage in the parentheses represents theimprovement obtained by an alignment technique with respect to the original error. Figure 5 shows a synchronization result with a synthetic trajectory. The performance of the RCB, STE and the proposed techniques are compared. It is clear that the proposed technique outperformed the other techniques. Performance improvement of the proposed technique over existing techniques
3.2.Real Data EvaluationFor the real video test, we use two videos (54 frames and 81 frames long, respectively) capturing the activity of lifting a coffee cup by different people. We tracked the coffee cup that can represent the activity in a video to generate feature trajectories. Since ground-truth information is not available, we used visual judgement to assess whether the alignment was correct or not. Figure 6 shows some representative aligned frames in the 4th, 8th, and 12th elements of the alignment warp computed using the STE and the proposed technique. Note that if the coffee cup is at the same position in two frames, we marked it as “matched,” otherwise, “mismatched.” In the results obtained using the STE technique, only one pair of frames is matched, indicating that such technique can often result in erroneous alignments. The performance of the proposed technique is shown in the last two rows. It is observed that all the alignments are correct. 4.ConclusionsAn efficient technique is proposed to synchronize video sequences captured from planar scenes and related by varying temporal offsets. The proposed UBDTW technique is able to remove the biasing and lead to accurate temporal alignment. In the future, we would like to extend this work to more general scenes. ReferencesY. Caspi and M. Irani,
“Spatio-temporal alignment of sequences,”
IEEE Trans. Pattern Anal. Mach. Intell, 24
(11), 1409
–1424
(2002). https://doi.org/10.1109/TPAMI.2002.1046148 Google Scholar
L. Lee, R. Romano, and G. Stein,
“Monitoring activities from multiple video streams: establishing a common coordinate frame,”
IEEE Trans. Pattern Anal. Mach. Intell, 22
(8), 758
–767
(2000). https://doi.org/10.1109/34.868678 Google Scholar
M. A. Giese and T. Poggio,
“Morphable models for the analysis and synthesis of complex motion patterns,”
Int. J. Comput. Vis., 38
(1), 59
–73
(2000). https://doi.org/10.1023/A:1008118801668 Google Scholar
C. Rao, A. Gritai, M. Shah, and T. F. S. Mahmood,
“View-invariant alignment and matching of video sequences,”
Proc. ICCV03, 939
–945 2003). Google Scholar
M. Singh, I. Cheng, M. Mandal, and A. Basu,
“Optimization of symmetric transfer error for sub-frame video synchronization,”
Proc. ECCV03, 554
–567 2008). Google Scholar
R. I. Hartley and A. Zisserman, Multiple View Geometry in Computer Vision, 2nd ed.Cambridge University Press, Cambridge, UK
(2004). Google Scholar
|