High-precision synchronization of video cameras using a single binary light source

Qi Zhao; Yan Qiu Chen

doi:10.1117/1.3247860

1 October 2009 High-precision synchronization of video cameras using a single binary light source

Qi Zhao, Yan Qiu Chen

Author Affiliations +

Journal of Electronic Imaging, Vol. 18, Issue 4, 040501 (October 2009). https://doi.org/10.1117/1.3247860

Abstract

Camera synchronization is necessary for multicamera applications. We propose a simple and yet effective approach termed random on-off light source (ROOLS) to synchronize video sequences. It uses a single light source such as an LED to generate a random binary valued signal that is captured by the video cameras. The captured binary-valued sequences are then matched and the temporal offset of the cameras is computed up to subframe interval precision. We test the proposed method on synchronizing video sequences captured under a variety of illumination conditions and the results are verified against the ground truth provided by an LED array clock. The main contribution of the proposed method is that it reliably achieves high-precision synchronization at a low cost of only adding a simple light source. In addition, it is suited for synchronization in both laboratory and outdoor environments.

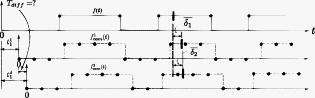
1. Introduction

For multicamera systems, synchronization is a must to provide accurate temporal correlation for incorporating image information from multiple viewpoints.

Synchronicity can be achieved through real-time hardware synchronization¹ or by establishing a time relationship between sequences recorded by unsynchronized video cameras.² While ensuring high precision synchronization, hardware solutions are costly and complex.

In a scenario where synchronous video sequences provided by hardware are not feasible, it is still possible to obtain synchronicity using image features.^{3, 4, 5} These feature-based methods depend on the existence of salient and robust features in the scene. The failure of such features to exist in the scene and the error of detecting, tracking, and matching them would lead to incorrect synchronization.

In this paper, we present a simple and yet effective method, termed random on-off light source (ROOLS), to recover the temporal offset at subframe accuracy. It utilizes an auxiliary light source such as an LED to provide temporal cues. Compared to special-purpose hardware approaches, our method is far less complex and is inexpensive. Compared to feature-based approaches, ROOLS is more robust since it is completely independent of scene properties.

2. Problem Statement

Without loss of generality, we consider the case of two video cameras. Let the time instances of the video frames taken by the $α$ ’th camera be denoted by

Eq. 1

T^{α} = (t_{1}^{α}, t_{2}^{α}, \dots, t_{N_{α}}^{α}), α ∊ {1, 2}, N_{α} ∊ N,

where

N_{α}

denotes the length of the

α

’th sequence, and

t_{k}^{α}

denotes the time of the

k

’th frame in the

α

’th sequence. Note that

T^{1}

and

T^{2}

are measured by a common clock.

In a typical situation, identical video cameras of constant frame interval $Δ T$ are used, when

Eq. 2

T^{α} = (t_{1}^{α}, t_{1}^{α} + Δ T, \dots, t_{1}^{α} + (N_{α} - 1) \times Δ T) .

Synchronizing two video sequences in such situation is equivalent to measuring the temporal offset between their initial frames

Eq. 3

T_{diff} = t_{1}^{1} - t_{1}^{2} .

3. Proposed Method

3.1.

Formulation

We propose to use a single temporally coded light source such as an LED as the signal to be captured by the cameras for synchronization. The light signal is essentially a time-continuous binary-valued function denoted as

Eq. 4

f : R \mapsto {0, 1} .

It is sampled at

T^{α}

by the

α

’th camera, producing a time-discrete binary-valued sequence

Eq. 5

{[f_{cam}^{α} (n)]}_{n = 1}^{N_{α}} = {[f (t_{n}^{α})]}_{n = 1}^{N_{α}} = {f [(n - 1) Δ T + t_{1}^{α}]}_{n = 1}^{N_{α}} .

Since

f

is binary valued, it can be characterized by time instants where its function value rises from 0 to 1 or drops from 1 to 0. We term each of these instants a transition event. Let

Φ

denote a subsequence of all transition events in

f

,

Eq. 6

Φ = (ϕ_{1}, ϕ_{2}, \dots, ϕ_{N}) .

For each

ϕ_{k}

, we have

Eq. 7

\forall ϵ > 0, f (ϕ_{k} - ϵ) \oplus f (ϕ_{k} + ϵ) = 1,

where ⊕ denotes the exclusive or operator, and

ϵ

is an arbitrarily small real positive number. For the

α

’th camera, let

Φ^{α}

denote the transition events corresponding to

Φ

. Obviously, as part of

T^{α}

,

Φ^{α}

can be expressed as follows:

Eq. 8

Φ^{α} = [t_{I^{α} (1)}^{α}, t_{I^{α} (2)}^{α}, \dots, t_{I^{α} (N)}^{α}],

where

I^{α}

is a subsequence of

(1, 2, \dots, N_{α})

. For each

I^{α} (k)

, it satisfies

Eq. 9

f_{cam}^{α} [I^{α} (k)] \oplus f_{cam}^{α} [I^{α} (k) - 1] = 1 .

This notation and their relationship are illustrated in Fig. 1 .

Fig. 1

Achieving subframe-interval estimation: (1) the transition events of $f$ , $f_{cam}^{1}$ , and $f_{cam}^{2}$ are highlighted by black dots; (2) black vertical bars denote the mean position of corresponding transition events in $f$ , $f_{cam}^{1}$ , and $f_{cam}^{2}$ .

3.2.

Achieving Sub-Frame-Interval Precision

Given $Φ$ and $Φ^{α}$ , consider the difference between a pair of corresponding transition events:

Eq. 10

δ_{k}^{α} = Φ_{k}^{α} - Φ_{k} = t_{I^{α} (k)}^{α} - ϕ_{k} .

Provided that

δ_{k}^{α}

is an independent and identically distributed (i.i.d.) random variable uniformly distributed over

[0, Δ T]

with mean and variance being

μ = Δ T ∕ 2

and

σ^{2} = Δ T^{2} ∕ 12

. The averaged difference

\bar{δ_{α}} = 1 ∕ N \sum_{k = 1}^{N} δ_{k}^{α}

is a random variable with mean and variance being

\tilde{μ} = μ

and

{\tilde{σ}}^{2} = (1 ∕ N) σ^{2}

. However,

Eq. 11

\bar{δ_{α}} = \frac{1}{N} \sum_{k = 1}^{N} [t_{I^{α} (k)}^{α} - ϕ_{k}] = \bar{t_{I^{α}}} - \bar{ϕ},

where

\bar{t_{I^{α}}}

and

\bar{ϕ}

are the mean positions of transition events with respect to

f_{cam}^{α}

and

f

, as illustrated by Fig. 1. According to central limit theorem,⁶ the averaged sum of a sufficiently large number of i.i.d. random variables each with finite mean and variance approximates normal distribution. Hence,

\bar{δ_{α}}

takes a normal distribution with mean of

μ

and variance of

Δ T^{2} ∕ 12 N

. From Eq. 11 we obtain

Eq. 12

\bar{t_{I^{1}}^{1}} - \bar{t_{I^{2}}^{2}} = \bar{δ_{1}} - \bar{δ_{2}} .

Since

\bar{t_{I^{α}}^{α}} = (1 ∕ N) \sum_{k = 1}^{N} {t_{1}^{α} + [I^{α} (k) - 1]}

, Eq. 12 can be further written as

Eq. 13

where

T_{diff}^{'} = T_{diff} ∕ Δ T

,

δ^{'} = (\bar{δ_{1}} - \bar{δ_{2}}) ∕ Δ T \sim N (0, 1 ∕ 6 N)

. When

N

is sufficiently large, the variance of

δ^{'}

will be negligibly small, leading to high precision estimation of

T_{diff}^{'}

.

3.3.

Transition Detection Accuracy

In real-world applications, the binary sequence is obtained through quantifying the image intensity of the light source by certain threshold $τ$ . For samples crossing transition events, the quantified binary value might flip, causing the transition event to shift one frame backward. If we take a sample right before the edge where signal rises from 0 to 1 for instance, its intensity is close to 1 and incorrectly quantified to 1. Equation 13 tells us that the shift will introduce additional error to the estimation. Suppose the light source intensity is normalized and $τ = 0.5$ is chosen as the threshold so that the probabilities for transitions to flip from 0 to 1 and 1 to 0 are identical. Let $x_{i}^{α}$ denote a single shift event in a video sequence $α$ . Its probability density function (pdf) is $p (x_{i}^{α} = - 1) = p (x_{i}^{α} = 0) = 0.5$ , with expectation $μ_{x_{i}^{α}} = - 0.5$ and variance $σ_{x_{i}^{α}} = 0.25$ . Let $\bar{x^{α}} = (1 ∕ N) \sum_{i = 1}^{N} x_{i}^{α}$ denote averaged transition shift. Because $x_{i}^{α}$ are i.i.d. random variables, once again by the use of central limit theorem, we have $\bar{x^{α}} \sim N (- 0.5, 1 ∕ 4 N)$ . According to Eq. 13, the extra error $δ_{s}$ introduced by transition shift in two video sequences turns out to be $\bar{x^{1}} - \bar{x^{2}}$ . It can be proved that $δ_{s}$ takes a normal distribution with mean of 0 and variance of $1 ∕ 2 N$ . Counting in $δ_{s}$ , the total error of temporal offset estimation is

Eq. 14

δ = δ_{s} + δ^{'} ~ N (0, \frac{1}{1.5 N}) .

3.4.

Random Binary Sequence Design

The proposed method requires $δ_{k}^{α} = t_{I^{α} (k)}^{α} - ϕ_{k}$ to be i.i.d. random variables uniformly distributed in $[0, Δ T]$ . To achieve this, we set the transition time

Eq. 15

ϕ_{k} = ϕ_{k - 1} + χ,

where

ϕ_{k - 1}

is the time of the previous transition and

χ

is uniformly distributed in

[ι Δ T, (ι + κ) Δ T] \cdot ι, κ ∊ N

. Transition time generated in this way can be proved to ensure

δ_{k}^{α}

meeting the requirement.

3.5.

Transition Matching

The estimation of the temporal offset requires the transition events of the two cameras be matched. We refer to this process as transition matching. Let the segment

between two consecutive transition events be denoted as $D^{α} (k)$ :

Eq. 16

D^{α} (k) = {f_{cam}^{α} [I^{α} (k + 1)] - f_{cam}^{α} [I^{α} (k)]} \times [I^{α} (k + 1) - I^{α} (k)] .

The binary sequence

{[f_{cam}^{α} (n)]}_{n = 1}^{N_{α}}

can be equivalently represented by a sequence of transition segments. Let

λ (i, j) = | D^{1} (i) - D^{2} (j) |

denote the difference between two segments. Transition matching can be equivalently achieved by matching two sequences of transition segment. Based on the observation that the difference of corresponding segments would be small, optimal transition matching can be obtained by solving the following formula:

Eq. 17

\underset{l, i, j}{\arg \min} (\frac{\sum_{γ = 0}^{l - 1} λ (i + γ, j + γ)}{\max [\sum_{γ = 0}^{l - 1} | D^{1} (i + γ) |, \sum_{γ = 0}^{l - 1} | D^{2} (j + γ) |]} + \exp {- \frac{\sum_{γ = 0}^{l - 1} | D^{1} (i + γ) | + \sum_{γ = 0}^{l - 1} | D^{2} (j + γ) |}{2 \max [\sum_{k = 1}^{M_{1} - 1} | D^{1} (k) |, \sum_{k = 1}^{M_{2} - 1} | D^{2} (k) |]}}),

where

l

denotes the number of overlapping segments, and

M_{1}

and

M_{2}

are the lengths of the two segment sequences. The first term assesses the similarity of two overlapping segment sequences. Howerver, considering only the first term possibly leads to erroneous matching due to short overlapping length

l

. To avoid this, the second term is introduced to give a large penalty for small

l

. The optimal solution is sought by evaluating all combinations of

i

and

j

.

4. Experiments

4.1.

Hardware and Configuration

The experiment system is made up of two Sony HVR-V1 high-definition (HD) video cameras, an LED array clock providing the ground truth, and a single temporally encoded LED light source. The video cameras operate at 200 frames per second. The values of $ι$ and $κ$ in Eq. 15 are set to 2 and 6, which ensures there are at least two frames between adjacent transition events and avoids ambiguity in transition matching. We selected $τ = 0.5$ to quantize the image intensity of the LED a binary value.

4.2.

Experiment Results

We conducted three groups of experiments under illumination conditions including daylight, fluorescent lighting, and darkness. The results are shown in Table 1 . In all the tests, only 200 transition events were used. The average estimation error was about 0.08 frame intervals. We observe that all estimation errors are less than 0.2 frame intervals. This would be explained later.

Table 1

Results of 10 experiments.

Illum.	Estimated	Ground Truth	Error
Daylight	$- 3.410$	$- 3.2653$	0.1447
Daylight	0.6150	0.6000	0.0150
Daylight	0.5600	0.6122	0.0522
Fluorescent	$- 0.4900$	$- 0.6122$	0.1222
Fluorescent	0.1100	0	0.1100
Darkness	$- 2.9200$	$- 2.9605$	0.0405
Darkness	1.1150	1.1475	0.0325
Darkness	$- 2.8850$	$- 2.7961$	0.0889
Darkness	1.1900	1.3158	0.1258
Darkness	$- 2.7300$	$- 2.6273$	0.1027

4.3.

Comprison with Other Methods

The proposed method was compared with the feature-based approaches^{3, 4, 5} and the results are summarized in Table 2 . The comparison indicates ROOLS achieves higher estimation accuracy than existing approaches.

Table 2

Average temporal offset error of various approaches

	Method[3]	Method[4]	Method[5]	ROOLS
Averageerror	0.1	1	0.2	0.08

4.4.

Analysis and Discussions

The property of normal distribution states that 3 standard deviations from the mean account for about 99.7% of the distribution. When $N = 200$ transitions are used, according to Eq. 14, the standard deviation is about 0.05. The estimation error is bounded in $3 \times 0.05 = 0.15$ frame intervals. This explains why the estimation error in Table 1 are bounded in 0.2 frame intervals. The performance of the proposed method can be improved by increasing $N$ .

5. Conclusion

We presented an innovative approach toward synchronizing commercial video cameras. It achieved high-precision synchronization at the low cost of adding only a simple temporally coded light source. The proposed method requiring the video cameras to have identical frame rates is not a serious limitation since using identical video cameras for one task is convenient and typical.

Acknowledgments

The research work presented in this paper is supported by National Natural Science Foundation of China, Grant No. 60875024.

references

1.

T. Kanade, H. Saito, and S. Vedula, The 3D Room: Digitizing Time-Varying 3D Events by Synchronized Multiple Video Streams, (1998) Google Scholar

2.

A. Whitehead, R. Laganiere, and P. Bose, “Temporal synchronization of video sequences in theory and in practice,” 132 –137 (2005). Google Scholar

3.

Y. Caspi and M. Irani, “Spatio-temporal alignment of sequences,” IEEE Trans. Pattern Anal. Mach. Intell., 24 1409 –1424 (2002). https://doi.org/10.1109/TPAMI.2002.1046148 Google Scholar

4.

C. Rao, A. Gritai, M. Shah, and T. Syeda-Mahmood, “View-invariant alignment and matching of video sequences,” 939 –945 (2003). Google Scholar

5.

S. N. Sinha and M. Pollefeys, “Synchronization and calibration of camera networks from silhouettes,” 116 –119 (2004). Google Scholar

6.

W. Feller, An Introduction to Probability Theory and Its Applications, 2 Wiley, New York (1971). Google Scholar

Citation Download Citation

Qi Zhao and Yan Qiu Chen "High-precision synchronization of video cameras using a single binary light source," Journal of Electronic Imaging 18(4), 040501 (1 October 2009). https://doi.org/10.1117/1.3247860

Published: 1 October 2009

Access the abstract

JOURNAL ARTICLE
3 PAGES

DOWNLOAD PAPER SAVE TO MY LIBRARY

GET CITATION

CITATIONS

Cited by 5 scholarly publications and 3 patents.

Explore citations on Lens.org

RIGHTS & PERMISSIONS

Get copyright permission Get copyright permission on Copyright Marketplace

KEYWORDS

Cameras

Video

Light sources

Binary data

Content addressable memory

Light emitting diodes

Error analysis

1.

Introduction

2.

Problem Statement

Eq. 1

Eq. 2

Eq. 3

3.

Proposed Method

3.1.

Formulation

Eq. 4

Eq. 5

Eq. 6

Eq. 7

Eq. 8

Eq. 9

Fig. 1

3.2.

Achieving Sub-Frame-Interval Precision

Eq. 10

Eq. 11

Eq. 12

Eq. 13

3.3.

Transition Detection Accuracy

Eq. 14

3.4.

Random Binary Sequence Design

Eq. 15

3.5.

Transition Matching

Eq. 16

Eq. 17

4.

Experiments

4.1.

Hardware and Configuration

4.2.

Experiment Results

Table 1

4.3.

Comprison with Other Methods

Table 2

4.4.

Analysis and Discussions

5.

Conclusion

Acknowledgments

references

Show All Keywords

Keywords/Phrases

Search In:

Publication Years